Normal distributionsformel - Lommeregner (Excel-skabelon)

Indholdsfortegnelse:

Anonim

Normal fordelingsformel (indholdsfortegnelse)

  • Formel
  • eksempler
  • Lommeregner

Hvad er normal distributionsformel?

Begrebet normal distribution anvendes i statistikker, og vi støder på forskellige former for distribution i statistik. En sådan distribution og den mest anvendte distribution er den normale distribution, der har følgende egenskaber:

  • Middelværdien, medianen og tilstanden for den normale fordeling er altid ens.
  • En normal kurve er symmetrisk.
  • Halvdelen af ​​værdien ligger på hver side af kurven i en normal fordeling, og det er grunden til, at det kaldes den klokkeformede kurve.

En formel for normal distribution er givet af:

Z = (X – µ) /∞

  • X = Værdi, der standardiseres
  • µ = Gennemsnit af fordelingen
  • ∞ = Standardafvigelse for fordelingen

Eksempler på normal distributionsformel (med Excel-skabelon)

Lad os tage et eksempel for at forstå beregningen af ​​normal distribution på en bedre måde.

Du kan downloade denne Normal Distribution Template her - Normal Distribution Template

Normal distributionsformel - eksempel # 1

X for en eksamen er 145, 9, og 30% af de studerende kunne ikke bestå eksamen. Testens gennemsnitlige score er 120 og standardafvigelsen er 17. Hvad var testens bestående score?

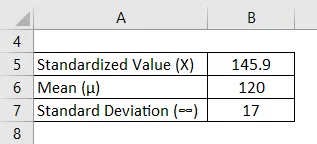
Løsning:

Normal distribution beregnes ved hjælp af nedenstående formel

Z = (X - µ) / ∞

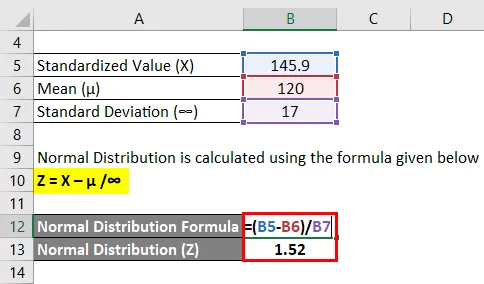
  • Normal distribution (Z) = (145, 9 - 120) / 17
  • Normal distribution (Z) = 25, 9 / 17
  • Normal distribution (Z) = 1, 52

Normal fordelingsformel - eksempel # 2

Den månedlige regning med vand i landsbyen Hyderabad distribueres normalt, og den har et gennemsnit på Rs. 225 og en standardafvigelse for Rs. 55. Disse mennesker tilbringer meget af deres tid i markerne vanding af planten. Hvor mange kunder kan forventes at have en regning på Rs i en gruppe på 500 kunder. 100 eller mindre?

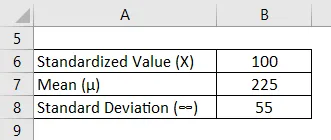
Løsning:

Normal distribution beregnes ved hjælp af nedenstående formel

Z = (X - µ) / ∞

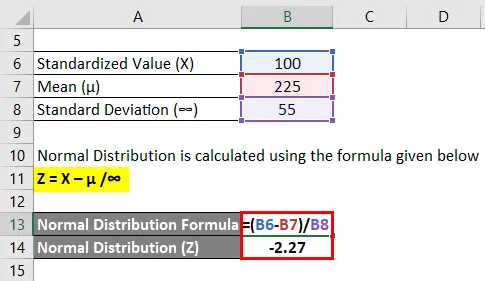
  • Normal distribution (Z) = (100 - 225) / 55
  • Normal distribution (Z) = -125 / 55
  • Normal distribution (Z) = -2, 27

Normal fordelingsformel - eksempel # 3

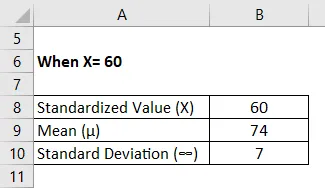
I en engelsk test udført i et klasseværelse på 100 studerende fordeles den score, som studerende opnår, normalt i datasættet. Imidlertid viste testens gennemsnitskarakter at være 74 og standardafvigelsen på 7. Hvilken andel af klassen forventes at have en score mellem 60 og 80?

Løsning:

For X = 60

Normal distribution beregnes ved hjælp af nedenstående formel

Z = (X - µ) / ∞

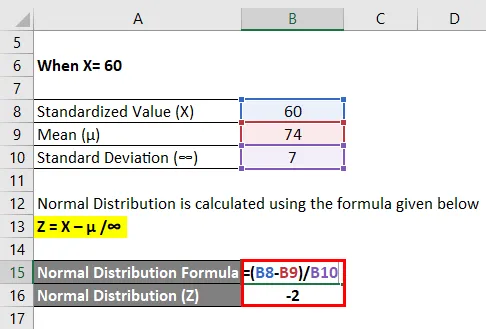
  • Normal distribution (Z) = (60 - 74) / 7
  • Normal distribution (Z) = -14 / 7
  • Normal distribution (Z) = -2

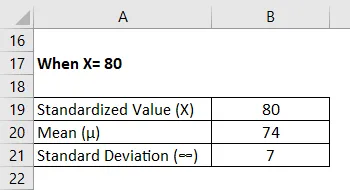
For X = 80

Normal distribution beregnes ved hjælp af nedenstående formel

Z = (X - µ) / ∞

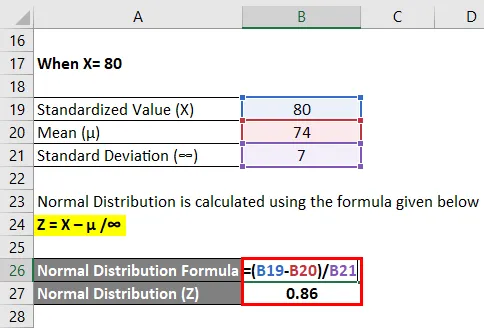
  • Normal distribution (Z) = (80 - 74) / 7
  • Normal distribution (Z) = 6/7
  • Normal distribution (Z) = 0, 86

Forklaring af normal distribution

Når man går til formlen i detaljer, trækkes en tilfældig variabel, der standardiseres, fra gennemsnittet af fordelingen og divideres derefter med standardafvigelsen for fordelingen. Når disse betingelser er bestemt, kan vi blot beregne Z-score, der også kaldes den normale standardfordeling.

Relevans og anvendelser af normal distributionsformel

  • En normal fordeling bruges i statistikker og i naturvidenskabsindustrien til repræsentation af de reelt værdsatte tilfældige variabler.
  • Teorien om normal distribution er også meget anvendt inden for videnskab som astronomi, fotonik og kvantemekanik. Grundlæggende er det et mål for spredningen af ​​den normale sandsynlighedsfordeling.
  • Teorien om normal distribution er også meget anvendt i finansverdenen, hvor den anvendes på aktivpriserne og afvigelsen af ​​aktivprisen fra gennemsnittet eller medianen bedømmes, og årsagen til sådan afvigelse undersøges detaljeret
  • Den normale fordelingsformel bruges også i undersøgelsen af ​​bestemmelse af skævheden og kurtosen for sandsynlighedsfordelingen i en given form eller art. Selv om det i virkeligheden er meget usandsynligt, at de fleste af prisfordelingerne er normale.

Normal distributionskalkulator

Du kan bruge følgende normal distributionskalkulator

x
μ
∞
Z

Z =
X - µ
=
∞
0-0
= 0
0

Anbefalede artikler

Dette har været en guide til Normal Distribution Formula. Her diskuterer vi, hvordan man beregner normal distribution sammen med praktiske eksempler. Vi leverer også normal distributionskalkulator med downloadbar excel-skabelon. Du kan også se på de følgende artikler for at lære mere -

  1. Beregning af DPMO-formlen
  2. Hvordan beregnes kapitaldækningsforhold?
  3. Beregning af relativ risikoreduktion
  4. Udnyttelsesforholdsformel