
Bestemmelseskoefficient (indholdsfortegnelse)
- Formel
- eksempler
Hvad er formlen for bestemmelseskoefficient?
I statistikker er koefficienten for bestemmelse, også kaldet R2, et værktøj, der bestemmer og vurderer evnen til en statistisk model til at forklare og forudsige fremtidige resultater. Med andre ord, hvis vi har afhængig variabel y og uafhængig variabel x i en model, hjælper R2 med at bestemme variationen i y med variation x. Det er en af de vigtigste output i regressionsanalyse og bruges, når vi vil forudsige fremtid eller teste nogle modeller med relateret information. Værdien af R2 ligger mellem 0 og 1 og højere værdien af R2, bedre vil modellen være forudsigelse og styrke. R2 ligner meget korrelationskoefficienten, da korrelationskoefficienten måler den direkte tilknytning af to variabler. R2 er dybest set et kvadrat af en korrelationskoefficient.
Formel til bestemmelseskoefficient:
Der er flere formler til beregning af bestemmelseskoefficient:
- Brug af korrelationskoefficient:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Hvor:
- X - Datapunkter i datasæt X
- Y - Datapunkter i datasæt Y
- X m - Gennemsnit for datasæt X
- Y m - Gennemsnit for datasæt Y
Så
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Brug af regressionsudgange
Bestemmelseskoefficient (R2) = forklaret variation / total variation
Bestemmelseskoefficient (R2) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Hvor:
- TSS - Summen af kvadrater = Σ (Yi - Ym) 2
- MSS - Model sum af kvadrater = Σ (Y - Ym) 2
- RSS - Rest sum af kvadrater = Σ (Yi - Y ^) 2
Y er den forudsagte værdi af modellen, Yi er ith-værdien og Ym er middelværdien
Eksempler på formel for bestemmelseskoefficient (med Excel-skabelon)
Lad os tage et eksempel for at forstå beregningen af bestemmelseskoefficienten på en bedre måde.
Du kan downloade denne bestemmelseskoefficientformel Excel-skabelon her - Bestemmelseskoefficientformel Excel-skabelonBestemmelseskoefficient - Eksempel nr. 1
Lad os sige, at vi har to datasæt X & Y, og hver indeholder 20 tilfældige datapunkter. Beregn bestemmelseskoefficienten for datasættet X & Y.
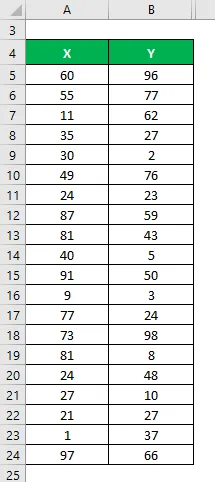
Gennemsnit beregnes som:
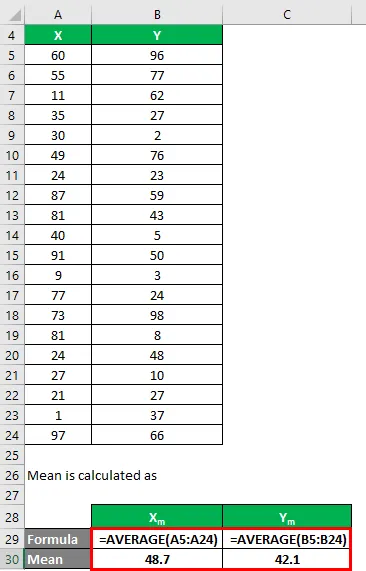
- Gennemsnit af datasæt X = 48, 7
- Gennemsnit af datasæt Y = 42.1
Nu skal vi beregne forskellen mellem datapunkter og middelværdien.
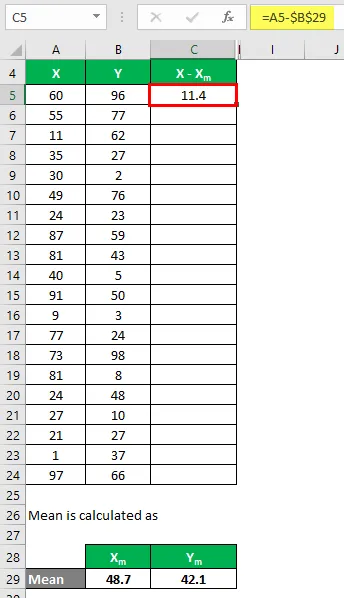
Beregn ligeledes for alle datasættene til X.
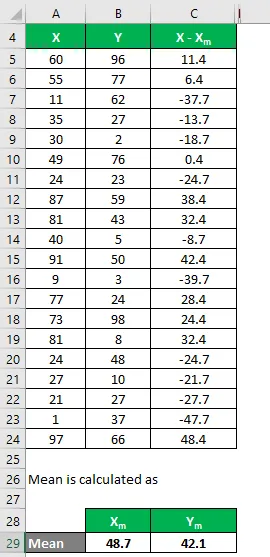
På samme måde beregnes det også for datasæt Y.

Beregn kvadratet af forskellen for både datasættet X og Y.
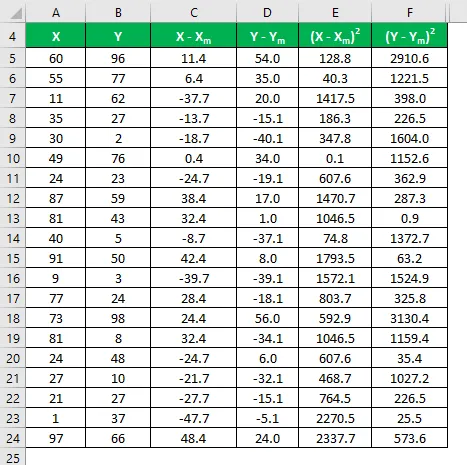
Multiplicer forskellen i X med Y.
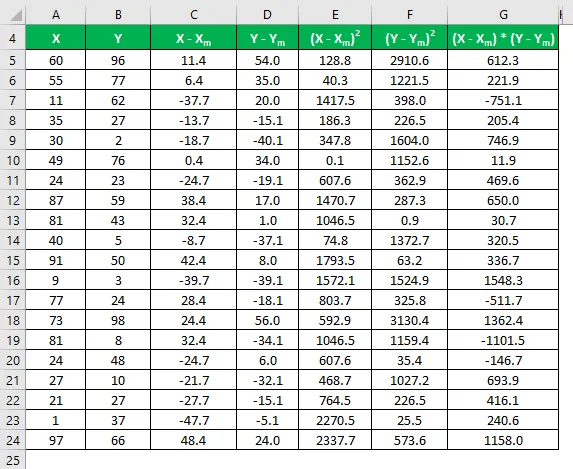
Korrelationskoefficient beregnes ved hjælp af nedenstående formel
Korrelationskoefficient = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
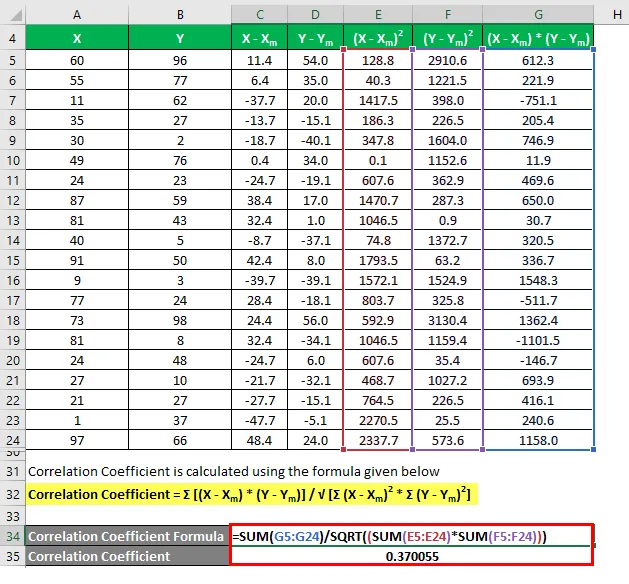
Bestemmelseskoefficient beregnes ved hjælp af nedenstående formel
Bestemmelseskoefficient = (korrelationskoefficient) 2
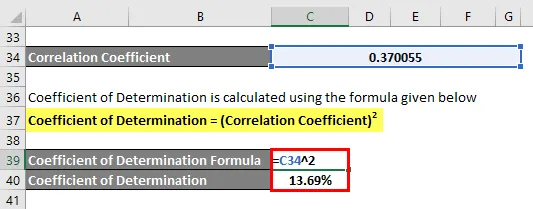
Bestemmelseskoefficient = 13, 69%
Bestemmelseskoefficient - Eksempel # 2
Lad os sige, at du er en meget risikovillig investor, og du ønsker at investere penge på aktiemarkedet. Du er ikke sikker på, hvilke aktier du skal investere i, og din risikoappetit er også lav. Så du vil investere i en aktie, der er sikker og kan efterligne indekstens resultater. Din ven, der er en aktiv investor, har listen over 3 aktier til dig baseret på deres grundlæggende og tekniske oplysninger, og du vil vælge 2 aktier blandt disse tre.
Du har også samlet oplysninger om deres historiske afkast i de sidste 15 år.
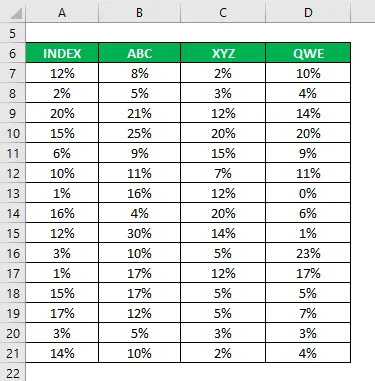
Korrelationskoefficient beregnes ved hjælp af excel-formlen
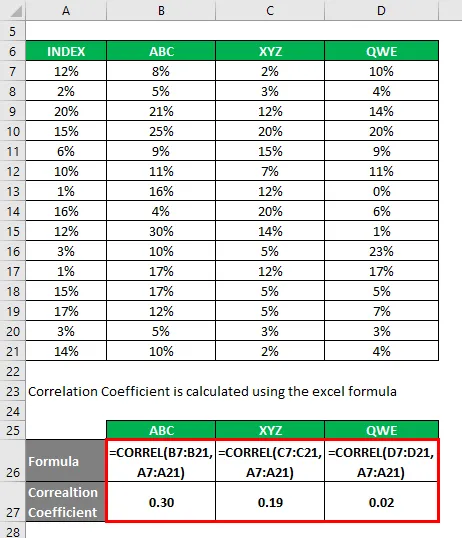
Bestemmelseskoefficient beregnes ved hjælp af nedenstående formel
Bestemmelseskoefficient = (korrelationskoefficient) 2
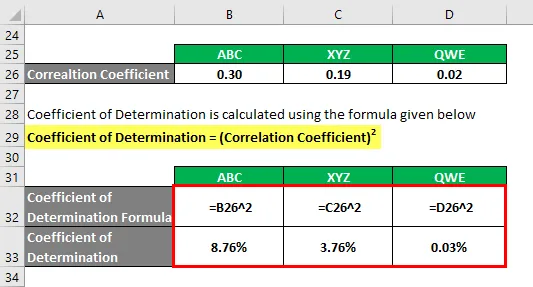
Baseret på informationen vælger du aktie ABC og XYZ at investere, da de har den højeste bestemmelseskoefficient.
Forklaring
Som forklaret ovenfor er bestemmelseskoefficienten kvadratet for korrelationen mellem to datasæt. Hvis R2 er 0, betyder det, at der ikke er nogen sammenhæng, og uafhængig variabel kan ikke forudsige værdien af den afhængige variabel. På samme måde, hvis dens værdi er 1, betyder det, at uafhængig variabel altid vil være en succes med at forudsige den afhængige variabel. Men der er også nogle begrænsninger. Selvom det fortæller os sammenhængen mellem 2 datasæt, fortæller det os ikke, om denne værdi er nok eller ej.
Stor værdi R2 betyder heller ikke altid, at de 2 variabler har stærke forhold, og det kan være en fluke. For eksempel: Lad os sige, at R2-værdien mellem et antal biler, der sælges i et år, og antallet af iskasser, der sælges på et år, er 80%. Men der er ingen sammenhæng mellem disse to. Så man skal være meget forsigtig, mens man bruger R2 og først forstå dataene og derefter anvende metoden
Relevans og anvendelser af bestemmelseskoefficientformel
Der er mange praktiske anvendelser af R 2 . For eksempel bruges R2 meget ofte af investorer til at sammenligne ydeevnen i deres portefølje med markedet og forsøge at forudsige fremtidige retninger. Tilsvarende hjælper hedgefonde med R 2 dem til at modellere risikoen i deres modeller. Men i sidste ende er resultatet baseret på rene tal og statistikker, der undertiden kan være vildledende. Som nævnt ovenfor skal man først kontrollere, om output fra R 2 giver mening i det virkelige liv eller ej.
Anbefalede artikler
Dette har været en guide til formel for bestemmelseskoefficient. Her diskuterer vi, hvordan man beregner bestemmelseskoefficienten sammen med praktiske eksempler og downloadbar excel-skabelon. Du kan også se på de følgende artikler for at lære mere -
- Vejledning til markedsrisikopremier
- Eksempler på formel for dækningsforhold
- Regnemaskine til aktivitetsbaseret omkostningsformel
- Hvordan beregnes informationsforhold ved hjælp af formler?