
Introduktion til Inline-funktion i Matlab
Inline-funktioner i Matlab har to kategorier, den ene er indbyggede funktioner, og den anden bruges definerede funktioner, der oprettes af brugeren.
Indbyggede funktioner
Matlab har mange indbyggede funktioner kvadratrod, sin, cos, tan, eksponentiel, log osv. Det har også mere komplekse og specielle matematiske funktioner som gammafunktioner og Bessel-funktioner. Det har også nogle indbyggede konstanter pi, I (komplekse tal) og uendelig.
Eksempel:
sin ( pi / 2 )
Det giver output som 1.
i dette eksempel nævnte vi ikke engang værdien af pi, automatisk tager pi værdien 3.14.
sqrt (3)
Det giver output 1, 73.
Og hvis skriv program erklæring sqrt (-1), vil det give ans som 0, 00 + i

Brugerdefinerede funktioner
Nøgleordet bruges til at definere vores egen funktion er "inline", lad nu se, hvordan du bruger det
Lad os antage, at jeg vil oprette en funktion sjov = x 2 - 6
Matlab-kommandoer vil være
Fun = inline ( ' x 2 – 6 ', ' x ' ) . . . . . . . . . . (1) function declaration and defination
Fun =
inline function :
Sjov = - 6.. . . . . . output fra (1)
Fun ( 1 ) (2) giving value x=1
Ans =
-5. . . .output af (2)
Fun ( 2 ) ….(3) giving value x=2
Ans =
-2. . . output fra (3)
Fun ( 3 ) . . . . . . . . . . . . . . . . . . . . (2) giving value x=3
Ans =
3.. . . . . . output fra (3)

- Matlab-funktioner fungerer på såvel skalaer som vektorer
- For at vinde inline-funktionsejre bruges 'vectorize' nøgleordet inde i funktionsdefinitionen.
- I ovenstående eksempel antager jeg, at jeg vil oprette vektorfunktion 'sjov', så vil kommandoer være
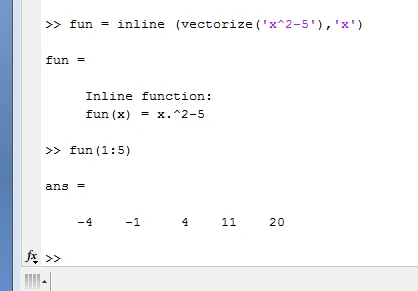
Fun = inline ( vectorize ( ' x 2 – 5 ', ' x ' )
Det vil skabe vektor sjov.
Fun ( 1 : 5 )
And evolution will take values of x as 1, 2, 3, 4 and 5
Output til dette program vil være
-4 -1 4 11 og 20
I denne første værdi er for x = 1, anden værdi er for x = 2, tredje værdi er for x = 3, frem-værdi er for x = 4 og femte værdi er for x = 5.
Syntaks for inline-funktion
Det er kategorier i tre dele.
1. Funktionsdefinition: I dette skriver vi funktionsstrengen og definerer den uafhængige variabel.
Function name = inline ( ' function ', ' independent variable ' )
Fun = inline ( ' x 2 – 5 ', ' x ' )
2. Funktionsudvikling: I dette vurderer vi funktion ved at give en hvilken som helst værdi til den uafhængige variabel.
Function name (variable value )
Fun ( 1 )
3. Vectorize-funktion: Denne funktion opretter en vektor for den givne funktion.
Function name = inline ( vectorize( ' function string ' ), ' independent variable ' )
Y = inline ( vectorize ( ' x 2 – 1 ' ), ' x ' )
eksempler
De følgende eksempler er som følger
Eksempel 1:
Lad os overveje en funktion
Z = x 3 - 56
For at løse ovennævnte ligning i Matlab er vi nødt til at oprette en inline-funktion for z og har brug for at tildele en uafhængig variabel.
Matlab-kode:
>>
z =
Inline function :
Z ( x ) = x . 3 - 56
>> z ( 0 )
Ans = 4
>> z ( 1 0 )
Ans = 996
>> z ( -1 )
Ans = 5
Eksempel 2:
Z = x 3 + 23 x - 9
Matlab-kode for eksempel 2
Z = inline ( vectorize ( ' x .^3 + 23*x – 9 ' ), ' x ' )
z =
Inline function :
Z ( x ) = x . 3 + 23 * x - 9
>> z ( 1 : 10 )
Ans = Kolonner 1 til 3
15 45 87
Kolonne 4 til 6
147 231 345
Kolonner 7 til 9
495 687 927
Kolonne 10
1221
>> z ( 1 : 0.5 : 5 )
Ans = Kolonner 1 til 4
15.0000 28.8750 45.0000 64.1250
Kolonner 5 til 8
87.0000 114.3750 147.0000 185.6250
Kolonne 9
231.0000
Konklusion - Inline-funktioner i Matlab
Inline-funktioner er globale, men det tager aldrig plads i Matlab-arbejdsområdet. Det fungerer som anonyme funktioner, men disse er ikke anonyme funktioner, fordi anonyme funktioner optager plads på tidspunktet for oprettelse af funktion. Inline-funktioner returnerer kun én værdi, selvom systemet håndterer arrays og matrix.
Anbefalede artikler
Dette er en guide til Inline-funktioner i Matlab. Her diskuterer vi Inline-funktioner i Matlab, Syntax og eksempler. Du kan også gennemgå vores andre relaterede artikler for at lære mere-
- Hvad er Matlab?
- Introduktion til Matlab
- Matlab-kommandoer
- Karriere i MATLAB
- Matlab Compiler | Anvendelser af Matlab Compiler
- Eksempler på Python-indbyggede funktioner