Lineær regression i Excel (indholdsfortegnelse)
- Introduktion til lineær regression i Excel
- Metoder til brug af lineær regression i Excel
Introduktion til lineær regression i Excel
Lineær regression er en statistisk teknik / metode, der bruges til at undersøge forholdet mellem to kontinuerlige kvantitative variabler. I denne teknik bruges uafhængige variabler til at forudsige værdien af en afhængig variabel. Hvis der kun er en uafhængig variabel, er det en simpel lineær regression, og hvis et antal uafhængige variabler er mere end én, er det multiple lineær regression. Lineære regressionsmodeller har et forhold mellem afhængige og uafhængige variabler ved at tilpasse en lineær ligning til de observerede data. Lineær henviser til det faktum, at vi bruger en linje til at passe til vores data. De afhængige variabler anvendt i regressionsanalyse kaldes også respons eller forudsagte variabler, og uafhængige variabler kaldes også forklarende variabler eller prediktorer.
En lineær regressionslinje har en ligning af typen: Y = a + bX;
Hvor:
- X er den forklarende variabel,
- Y er den afhængige variabel,
- b er linjens hældning,
- a er y-afskærmning (dvs. værdien af y når x = 0).
Metoden med mindst-kvadrater bruges generelt ved lineær regression, der beregner den bedste fit-line for observerede data ved at minimere summen af kvadrater for afvigelse af datapunkter fra linjen.
Metoder til brug af lineær regression i Excel
Dette eksempel lærer dig metoderne til udførelse af lineær regressionsanalyse i Excel. Lad os se på et par metoder.
Du kan downloade denne lineære regression Excel-skabelon her - Lineær regression Excel-skabelonMetode nr. 1 - Spredtdiagram med en trendline
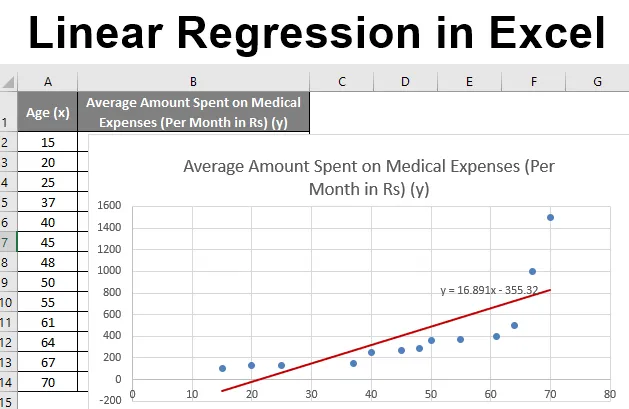
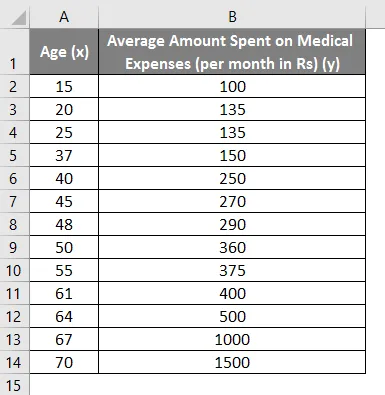
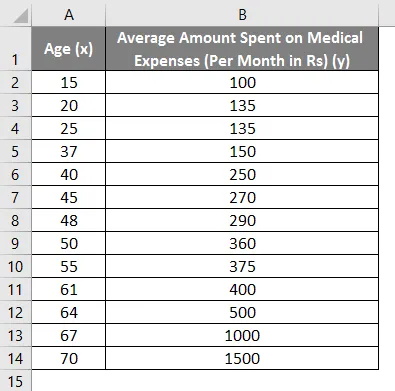
Lad os sige, at vi har et datasæt over nogle personer med deres alder, biomasseindeks (BMI) og det beløb, de bruger på medicinske udgifter i en måned. Nu med en indsigt i enkeltpersoners karakteristika som alder og BMI, ønsker vi at finde ud af, hvordan disse variabler påvirker de medicinske udgifter, og bruger derfor disse til at udføre regression og estimere / forudsige de gennemsnitlige medicinske udgifter for nogle specifikke individer. Lad os først se, hvordan kun alder påvirker medicinske udgifter. Lad os se datasættet:
Beløb på medicinske udgifter = b * alder + a
- Vælg de to kolonner i datasættet (x og y), inklusive overskrifter.
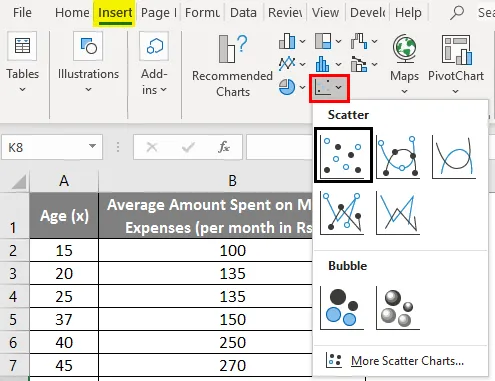
- Klik på 'Indsæt' og udvid dropdown for 'Scatter Chart' og vælg 'Scatter' miniature (første)
- Nu vises et scatter-plot, og vi tegner regressionslinjen på dette. For at gøre dette skal du højreklikke på et hvilket som helst datapunkt og vælge 'Tilføj trendline'
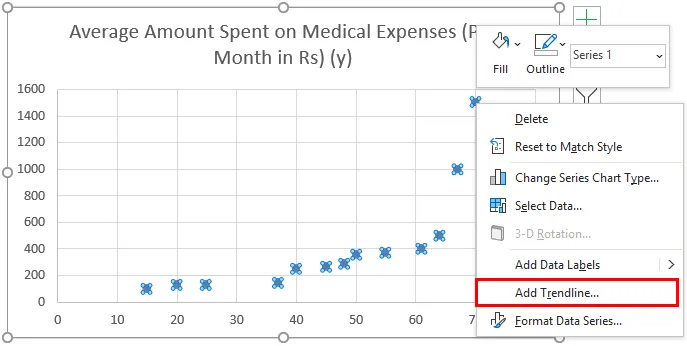
- I ruden 'Format Trendline' til højre skal du vælge 'Linear Trendline' og 'Display Equation on Chart'.
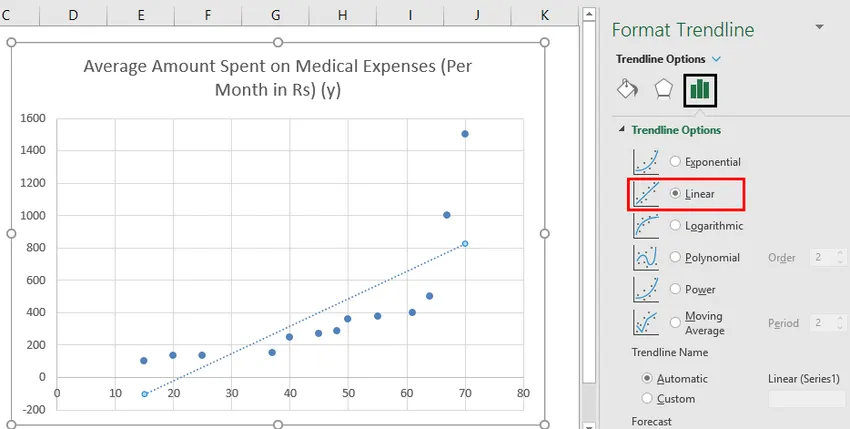
- Vælg 'Vis ligning på kort'.
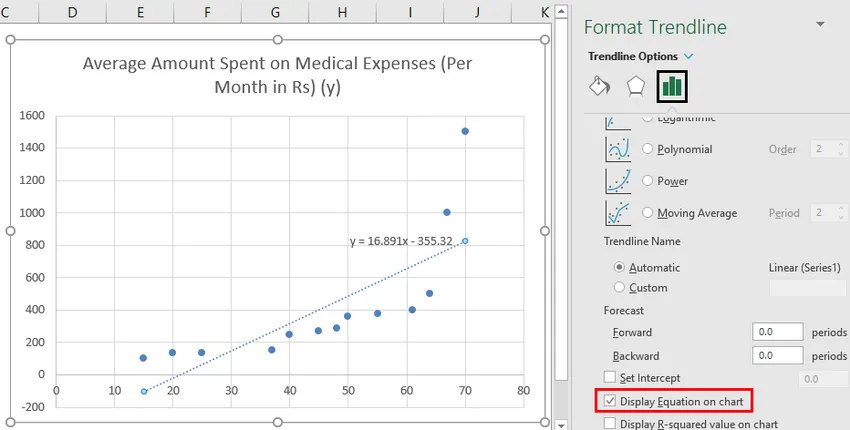
Vi kan improvisere skemaet i henhold til vores krav, som at tilføje aksetitler, ændre skala, farve og linjetype.
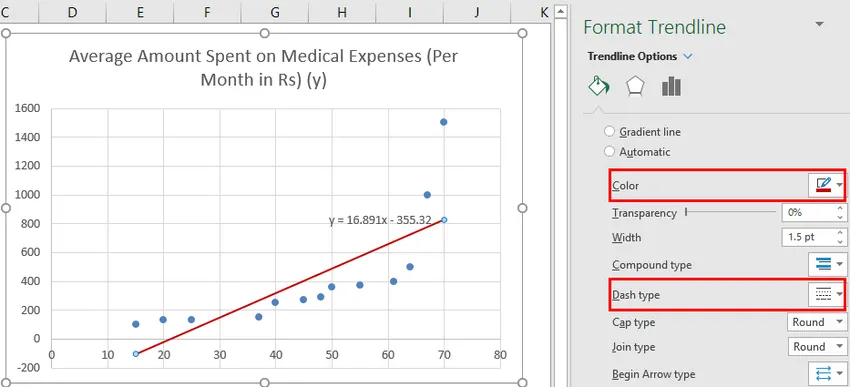
Efter improvisation af diagrammet er dette output, vi får.

Metode # 2 - AnalyseværktøjPak-tilføjelsesmetode
Analyse ToolPak er undertiden ikke aktiveret som standard, og vi er nødt til at gøre det manuelt. For at gøre det:
- Klik på menuen 'Filer'.
Klik derefter på 'Indstillinger'.
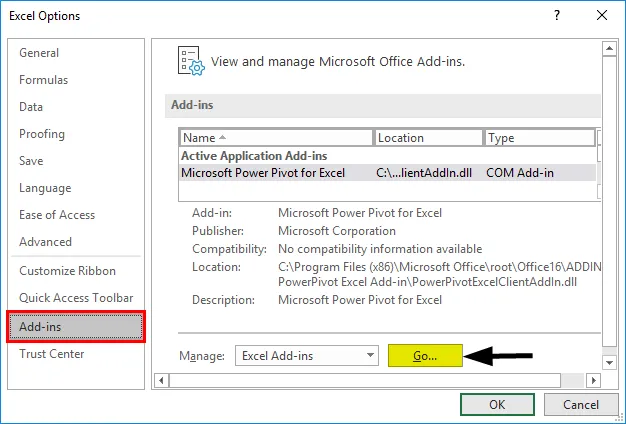
- Vælg 'Excel-tilføjelsesprogrammer' i boksen 'Administrer', og klik på 'Gå'
- Vælg 'Analyse ToolPak' -> 'OK'
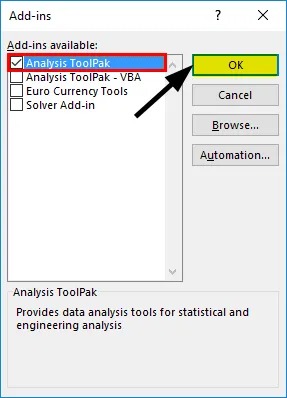
Dette tilføjer værktøjer til "Dataanalyse" til fanen "Data". Nu kører vi regressionsanalysen:
- Klik på 'Dataanalyse' under fanen 'Data'
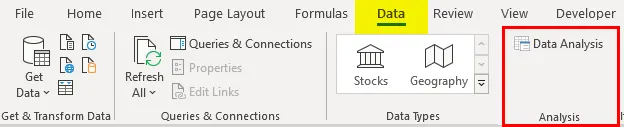
- Vælg 'Regression' -> 'OK'
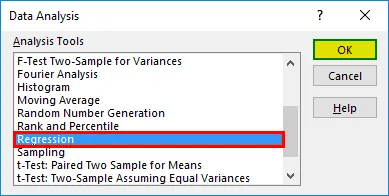
- En regressionsdialogboks vises. Vælg Input Y-området og Input X-området (henholdsvis medicinske udgifter og alder). I tilfælde af multiple lineær regression kan vi vælge flere kolonner med uafhængige variabler (som hvis vi ønsker at se effekten af BMI også på medicinske udgifter).
- Marker afkrydsningsfeltet 'Etiketter' for at inkludere overskrifter.
- Vælg den ønskede 'output' mulighed.
- Marker afkrydsningsfeltet 'rester' og klik på 'OK'.
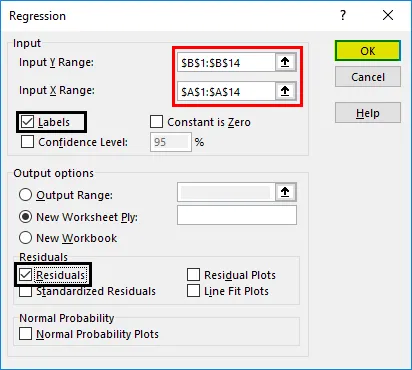
Nu bliver vores regressionsanalyseproduktion oprettet i et nyt regneark med angivelse af regressionsstatistikker, ANOVA, rester og koefficienter.
Output fortolkning:
- Regressionsstatistik fortæller, hvor godt regressionsligningen passer til dataene:
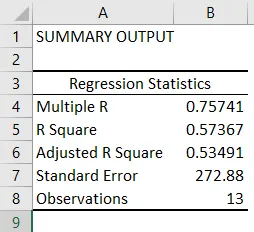
- Multipel R er korrelationskoefficienten, der måler styrken i det lineære forhold mellem to variabler. Det ligger mellem -1 og 1, og dets absolutte værdi viser forholdets styrke med en stor værdi, der indikerer stærkere forhold, lav værdi, der indikerer negativ og nulværdi, der indikerer intet forhold.
- R Square er den bestemmelseskoefficient, der bruges som en indikator for pasformens godhed. Det ligger mellem 0 og 1, med en værdi tæt på 1, hvilket indikerer, at modellen passer godt. I dette tilfælde forklares 0, 57 = 57% af y-værdierne med x-værdierne.
- Justeret R-firkant er R-kvadrat justeret for antallet af forudsigere i tilfælde af multiple lineær regression.
- Standard Error viser nøjagtigheden af regressionsanalyse.
- Observationer viser antallet af modelobservationer.
- Anova fortæller niveauet for variation i regressionsmodellen.

Dette bruges normalt ikke til simpel lineær regression. Imidlertid angiver 'Betydning F-værdierne', hvor pålidelige vores resultater er, med en værdi større end 0, 05, der antyder at vælge en anden prediktor.
- Koefficienter er den vigtigste del, der bruges til at opbygge regressionsligning.

Så vores regressionsligning ville være: y = 16.891 x - 355.32. Dette er det samme som det, der blev gjort ved metode 1 (scatterdiagram med en trendline).
Hvis vi nu ønsker at forudsige gennemsnitlige medicinske udgifter, når alderen er 72:
Så y = 16, 891 * 72 -355, 32 = 860, 832
Så på denne måde kan vi forudsige værdier af y for alle andre værdier af x.
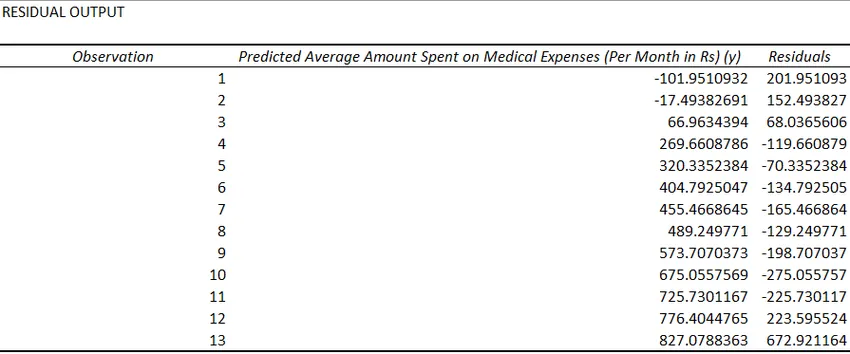
- Restpersoner angiver forskellen mellem faktiske og forudsagte værdier.
Den sidste metode til regression er ikke så almindeligt anvendt og kræver statistiske funktioner som hældning (), aflytning (), korrelering () osv. For at udføre regressionsanalyse.
Ting at huske på lineær regression i Excel
- Regressionsanalyse bruges generelt til at se, om der er et statistisk signifikant forhold mellem to sæt af variabler.
- Det bruges til at forudsige værdien af den afhængige variabel baseret på værdier for en eller flere uafhængige variabler.
- Hver gang vi ønsker at tilpasse en lineær regressionsmodel til en datagruppe, skal dataintervidden nøje overholdes, som om vi bruger en regressionsligning til at forudsige en værdi uden for dette interval (ekstrapolering), så kan det føre til forkerte resultater.
Anbefalede artikler
Dette er en guide til Lineær regression i Excel. Her diskuterer vi, hvordan man udfører Lineær regression i Excel sammen med praktiske eksempler og downloadbar excel-skabelon. Du kan også gennemgå vores andre foreslåede artikler -
- Sådan forberedes lønningslisten i Excel?
- Brug af MAX-formler i Excel
- Tutorials om cellehenvisninger i Excel
- Oprettelse af regressionsanalyse i Excel
- Lineær programmering i Excel