Lineær interpolation i Excel (indholdsfortegnelse)
- Hvad er interpolering?
- Interpolation med prognosefunktion i Excel
- Eksempler på lineær interpolering i Excel
Hvad er interpolering?
I matematikens verden er interpolering en metode til at oprette nye datapunkter ved hjælp af kendte datapunkter. Interpolering estimerer værdien baseret på de eksisterende tilgængelige dataværdier, der er relatable.
For eksempel - Hvis vi kører en cykel i 60 km / time og nåede en bestemt destination på 1 time, og hvis vi kører 45 km / time og nåede en bestemt destination på 45 minutter. Så hvor lang tid vil det tage at nå en destination, hvis vi kører 30 km / time.
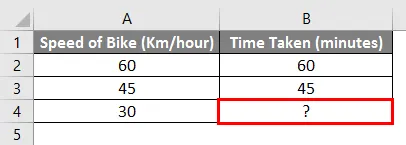
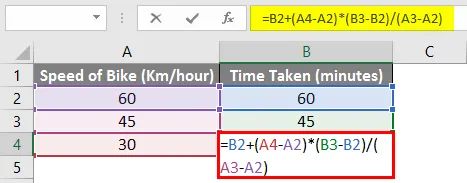
Ved hjælp af simpel matematik kan vi beregne de manglende værdier i ovenstående eksempel. Vi er nødt til at indsætte nedenstående formel i celle B4.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Så på baggrund af ovenstående formel kan vi sige, at det tager 30 minutter at nå destinationen, hvis vi kører med 30 km / time.
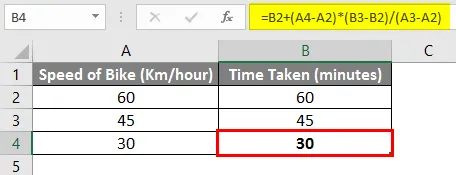
Lad os prøve at bryde den ovenstående formel og forstå formlen i detaljer.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
I ovenstående eksempel beregner det sidste afsnit af formlen, der er fremhævet med rødt, hvor lang tid det tager at ændre sig, hver gang cyklens hastighed ændres med 1. I vores eksempel ændres den tid, der tages med 1 minut, når cyklens hastighed ændres med 1 km /time.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Det andet afsnit (i blåt ovenfor) beregner, hvor langt vores cykelhastighed er væk fra den givne første hastighed på cyklen ganges derefter med den beregnet værdi ovenfor. Baseret på vores eksempel er det 30 (celle A4) minus 60 (celle A2), hvis resultat derefter ganges med 1 (hvilket svarer til -30).
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Endelig den første sektion af formlen (i brun ovenfor); tilføjer vi den første værdi af cyklens hastighed. I vores eksempel giver dette det endelige resultat på 60 + (-30) * (1) = 30 minutter. I skolen brugte vi nedenstående formel til at beregne den manglende værdi af Y.
Y = Y1 + (X-X1) * (Y2-Y1) / (X2 - X1)
Dette er et eksempel på, hvordan man beregner de manglende værdier ved hjælp af en manuel formel for at forstå interpolering.
Excel har en indbygget funktion, der udfører en lignende beregning som ovenfor, og den er kendt som FORECAST-funktion. Nu lærer vi denne funktion detaljeret nu.
Interpolering med prognosefunktion i Excel
Prognose er en regnearkfunktion, der er tilgængelig i MS Excel, og den bruger lineær regression til at finde ud af den manglende værdi. Prognose, som navnet antyder, bruges til at forudsige den fremtidige værdi af et datapunkt, men det kan også bruges til at interpolere en værdi. Grundlæggende bruges det til at beregne den fremtidige værdi baseret på de eksisterende værdier i et specifikt datasæt.
Syntaks for prognosefunktion

Argumenter for prognosefunktion:
- x - Det er et datapunkt, som vi vil vide den resulterende værdi for.
- Kendt_y's - Område af celler, der indeholder værdierne af Y.
- Kendt_x's - Celleområde, der indeholder værdierne af X.
I betragtning af det samme eksempel ovenfor, lad os prøve at bruge Prognose-funktionen.
I vores eksempel
x - Celle B4 (som vi vil finde ud af, hvor lang tid der er taget, når hastigheden er 30 km / time).
Known_y's - Cell B2 til Cell B3 (Tiden tager for den kendte cykelhastighed).
Known_x's - Cell A2 til Cell A3 (hastighed på den allerede givne cykel, som vi kender den tid, der er taget).
Så den endelige formel i celle B4 vil være som nedenfor:
= PROGNOSE (A4, B2: B3, A2: A3)
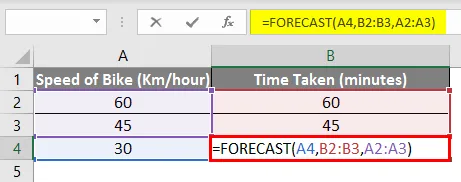
Og som du kan se, er det endelige resultat det samme, dvs. 30 minutter .
For at oprette et diagram skal du gå til menuen Indsæt, klikke på Spredning og derefter vælge Spredning med glatte linjer og markører.
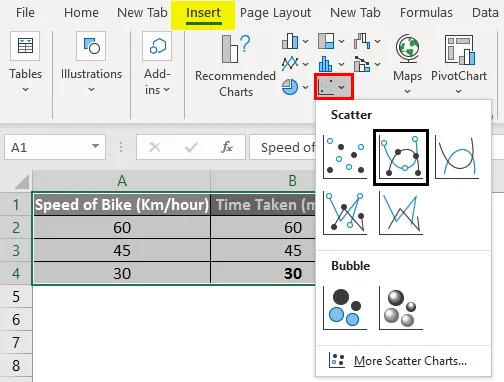
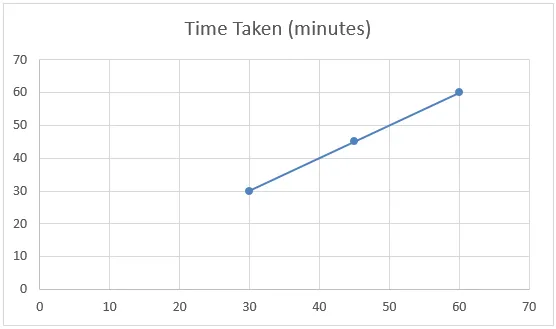
Hvis vi ser på nedenstående diagram i ovenstående eksempel, kan vi sige, at datasættet har et lineært forhold og kendt som lineær interpolering.
Eksempler på lineær interpolering i Excel
Lad os forstå den lineære interpolation i Excel med nogle eksempler.
Du kan downloade denne lineære interpolation Excel-skabelon her - Lineær interpolation Excel-skabelonEksempel 1
Antag, at du har salgs- og overskudsdata for tidligere år, og du vil vide overskuddet i det indeværende år, hvis du opnår et vist niveau af salg.
Se på nedenstående tabel. Du har salgsdata fra 2016 til 2018, og du vil vide, hvad der skal være overskuddet, hvis dit salg er Rs. 40.00.000 i 2019.
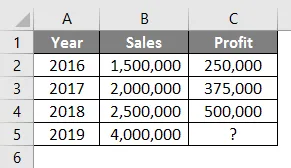
Så ved hjælp af Forecast-funktionen kan vi interpolere overskuddet fra 2019, når salget er Rs. 4.000.000
Formlen i celle C5 vil være som nedenfor:
= Prognose (B5, C2: C4, B2: B4)
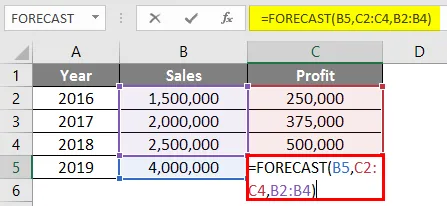
Efter brug af Prognosformel svaret vist nedenfor.
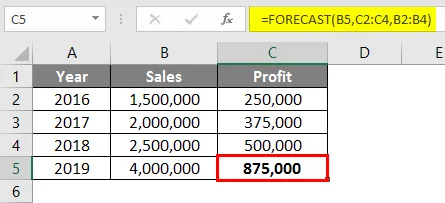
Resultatet for funktionen Prognose er Rs. 875.000 baseret på de tilgængelige salgs- og overskudsdata fra 2016 til 2018.
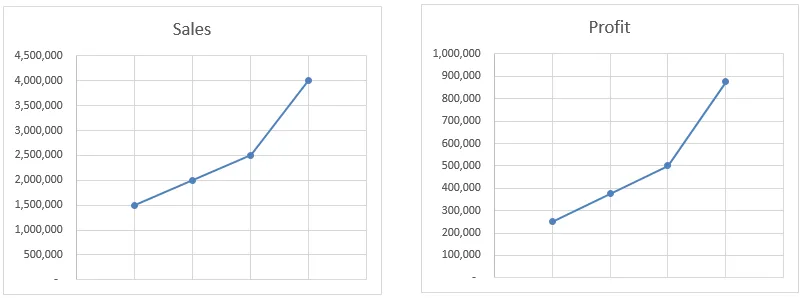
I dette eksempel interpolerer prognosefunktionen værdien baseret på alle tilgængelige data og ikke kun start- og slutpunkt. Som du kan se på diagrammerne, er overskuddet i bevægelse nøjagtigt det samme som salget. Selv hvis vi beregner værdien manuelt, vil den stadig give os det samme resultat.
Eksempel 2
Vi har data om de sidste 9 kampe i cricketholdet, som har vundet, og løb scoret af holdet.
Vi vil gerne finde ud af, hvor mange løb der er holdresultater, hvis 8 vagter falder.
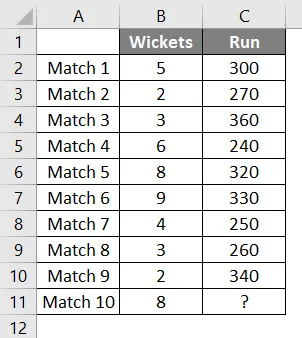
Så vi vil igen bruge den samme prognosefunktion som ovenfor.
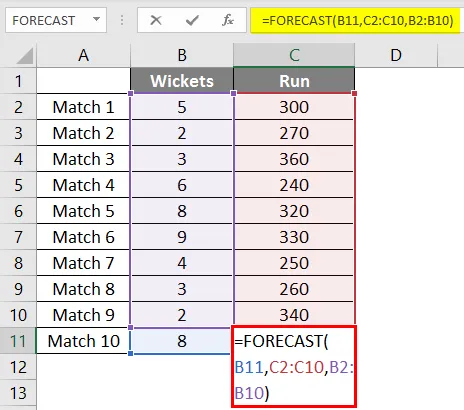
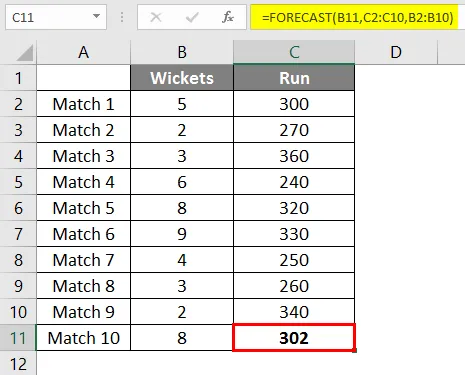
Når vi har anvendt formlen, får vi resultatet af 302 løb, hvis vi 8 wickets falder på grundlag af en lineær regression af de sidste 9 kampe spillet er spillet.
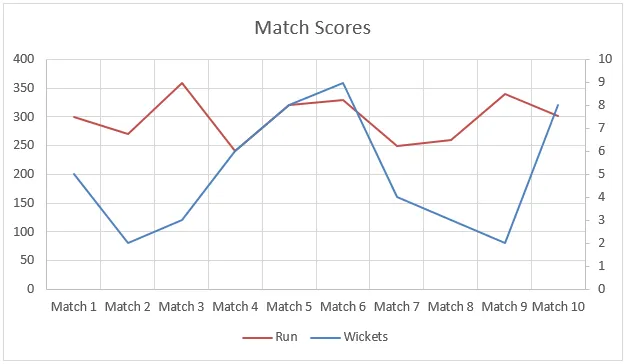
I dette eksempel var data ikke lineære, og du kan se det i nedenstående graf. Men alligevel hjalp Forecast-funktionen os med at interpolere kørslerne ved hjælp af data fra tidligere kampe.
Ting at huske på Lineær interpolation i Excel
- Prognosefunktion bruges til at forudsige / estimere værdien baseret på de eksisterende tilgængelige værdier, men den kan også hjælpe med at interpolere den manglende værdi.
- I tilfælde af, at data ikke er lineære, giver Forecast-funktionen dig ikke den nøjagtige værdi, der er baseret på lineær interpolering, men den giver dig den nærmeste værdi.
- Hvis x i prognosefunktionen er tekst eller ikke-numerisk, returnerer prognosefunktionen #VALUE-fejlen.
- Hvis Known_x og Known_y's ikke indeholder nogen data eller indeholder et andet sæt datapunkter, giver Prognosefunktion en # N / A-fejl.
- Hvis varensen af Kendte_x'er er nul, giver Forecast-funktionen # DIV / O-fejlen.
Anbefalede artikler
Dette er en guide til Lineær interpolation i Excel. Her diskuterer vi Sådan bruges lineær interpolation i Excel sammen med praktiske eksempler og downloadbar excel-skabelon. Du kan også gennemgå vores andre foreslåede artikler -
- Lineær regression i Excel
- Søg efter tekst i Excel
- Tekstformel i Excel
- Marimekko diagram Excel
- Interpolér i Excel
- Lineær programmering i Excel