Forskellen mellem lineær regression vs logistisk regression
Den følgende artikel Lineær regression vs logistisk regression giver de vigtigste forskelle mellem begge, men inden vi ser, hvad betyder regression?
Regression
Regression er dybest set et statistisk mål for at bestemme styrken i forholdet mellem en afhængig variabel, dvs. output Y og en række andre uafhængige variabler, dvs. X 1, X 2 og så videre. Regressionsanalyse bruges dybest set til forudsigelse og prognose.
Hvad er lineær regression?
Lineær regression er en algoritme, der er baseret på det overvågede læringsdomæne i maskinlæring. Det arver et lineært forhold mellem dets inputvariabler og den enkelte outputvariabel, hvor outputvariablen er kontinuerlig. Det bruges til at forudsige værdien af output, lad os sige Y fra inputene lad os sige X. Når kun enkelt input betragtes, kaldes det simpel lineær regression.
Det kan klassificeres i to hovedkategorier:
1. Enkel regression
Funktionsprincip: Hovedmålet er at finde ud af ligningen på en lige linje, der bedst passer til de samplede data. Denne ligning beskriver algebraisk forholdet mellem de to variabler. Den bedst passende lige linje kaldes regressionslinje.
Y = β 0 + β 1 X
Hvor,
β repræsenterer funktionerne
P 0 repræsenterer opsnittet
ß 1 repræsenterer koefficienten for træk X
2. Multivariabel regression
Det bruges til at forudsige en sammenhæng mellem mere end en uafhængig variabel og en afhængig variabel. Regression med mere end to uafhængige variabler er baseret på passende form til konstellationen af data på en flerdimensionel graf. Regressionens form skal være sådan, at den minimerer afstanden til formen fra hvert datapunkt.
En lineær sammenhængsmodel kan repræsenteres matematisk som nedenfor:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Hvor,
β repræsenterer funktionerne
P 0 repræsenterer opsnittet
ß 1 repræsenterer koefficienten for træk X1
β n repræsenterer koefficienten for træk Xn
Fordele og ulemper ved lineær regression
Nedenfor er fordele og ulemper:
Fordele
- På grund af dens enkelhed er det vidt brugt modellering til forudsigelser og konklusioner.
- Det fokuserer på dataanalyse og dataforarbejdning. Så det handler med forskellige data uden at bekymre sig om detaljerne i modellen.
Ulemper
- Det fungerer effektivt, når dataene normalt distribueres. For effektiv modellering skal kollineariteten således undgås.
Hvad er logistisk regression?
Det er en form for regression, der tillader forudsigelse af diskrete variabler ved en blanding af kontinuerlige og diskrete prediktorer. Det resulterer i en unik transformation af afhængige variabler, som ikke kun påvirker estimeringsprocessen, men også koefficienterne for uafhængige variabler. Det adresserer det samme spørgsmål, som multiple regression gør, men uden fordelingsmæssige antagelser på forudsigelserne. I logistisk regression er udgangsvariablen binær. Formålet med analysen er at vurdere virkningerne af flere forklaringsvariabler, som kan være numeriske eller kategoriske eller begge dele.
Typer af logistisk regression
Nedenfor er de 2 typer logistisk regression:
1. Binær logistisk regression
Den bruges, når den afhængige variabel er dikotom, dvs. som et træ med to grene. Det bruges, når den afhængige variabel er ikke-parametrisk.
Brugt når
- Hvis der ikke er nogen linearitet
- Der er kun to niveauer af den afhængige variabel.
- Hvis multivariat normalitet er tvivlsom.
2. Multinomial logistisk regression
Multinomial logistisk regressionsanalyse kræver, at de uafhængige variabler er metriske eller dikotomme. Det antager ikke antagelser om linearitet, normalitet og homogenitet af varians for de uafhængige variabler.
Det bruges, når den afhængige variabel har mere end to kategorier. Det bruges til at analysere relationer mellem en ikke-metrisk afhængig variabel og metriske eller dikotome uafhængige variabler og sammenligner derefter flere grupper gennem en kombination af binære logistiske regressioner. I sidste ende tilvejebringer det et sæt koefficienter for hver af de to sammenligninger. Koefficienterne for referencegruppen betragtes som alle nuller. Endelig foretages forudsigelse baseret på den højeste resulterende sandsynlighed.
Fordel ved logistisk regression: Det er en meget effektiv og udbredt teknik, da den ikke kræver mange beregningsressourcer og ikke kræver nogen indstilling.
Ulempe ved logistisk regression: Den kan ikke bruges til at løse ikke-lineære problemer.
Head to Head-sammenligning mellem Lineær Regression vs Logistic Regression (Infographics)
Nedenfor er de øverste 6 forskelle mellem Lineær Regression vs Logistisk Regression 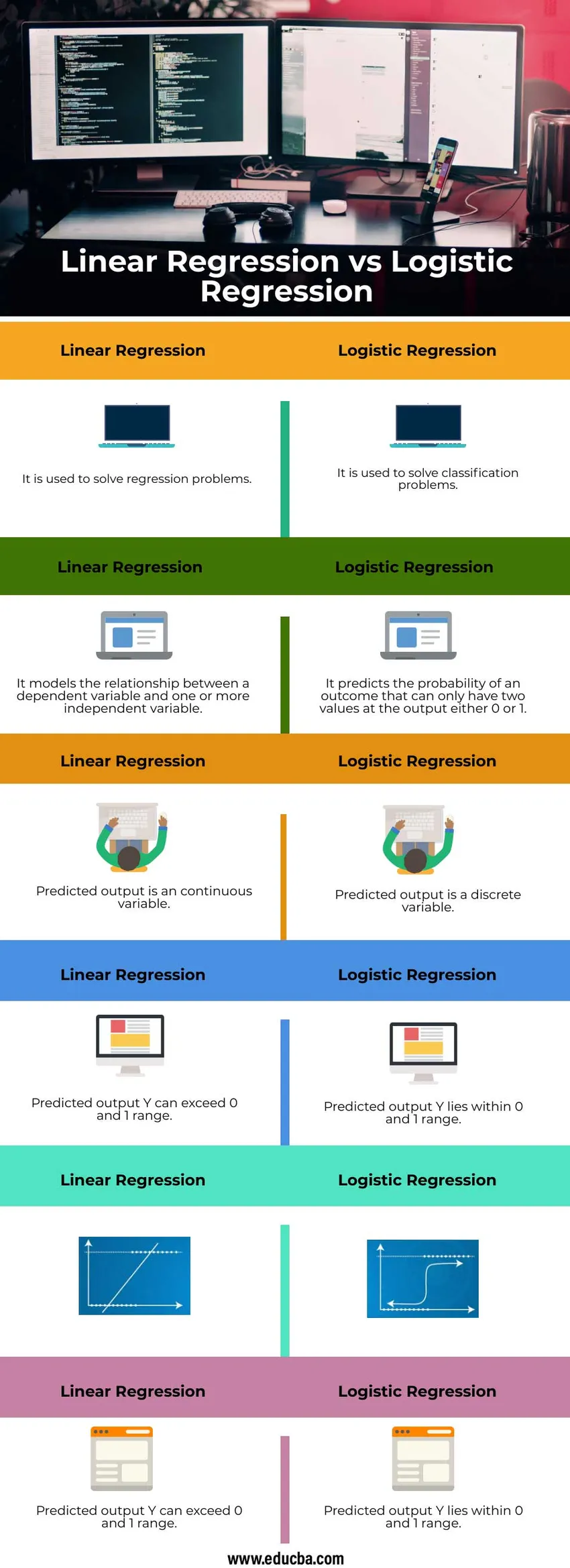
Nøgleforskel mellem den lineære regression vs logistisk regression
Lad os diskutere nogle af de vigtigste nøgleforskelle mellem Lineær regression vs logistisk regression
Lineær regression
- Det er en lineær tilgang
- Den bruger en lige linje
- Det kan ikke tage kategoriske variabler
- Det skal ignorere observationer med manglende værdier for den numeriske uafhængige variabel
- Output Y er angivet som
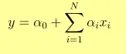
- 1 enhedsforøgelse i x øger Y med α
Applikationer
- Forudsigelse af prisen på et produkt
- At forudsige score i en kamp
Logistisk regression
- Det er en statistisk tilgang
- Den bruger en sigmoid-funktion
- Det kan tage kategoriske variabler
- Det kan tage beslutninger, selv om der er observationer med manglende værdier
- Output Y er angivet som, hvor z er angivet som
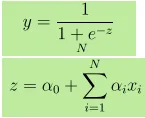
- 1 enhedsforøgelse i x øger Y ved log odds på α
- Hvis P er sandsynligheden for en begivenhed, er (1-P) sandsynligheden for, at den ikke forekommer. Odds for succes = P / 1-P
Applikationer
- At forudsige om det i dag regner eller ej.
- At forudsige, om en e-mail er en spam eller ej.
Lineær regression vs logistisk regression sammenligningstabel
Lad os diskutere den øverste sammenligning mellem Lineær regression vs logistisk regression
|
Lineær regression |
Logistisk regression |
| Det bruges til at løse regressionsproblemer | Det bruges til at løse klassificeringsproblemer |
| Den modellerer forholdet mellem en afhængig variabel og en eller flere uafhængige variabler | Det forudsiger sandsynligheden for et resultat, der kun kan have to værdier ved output enten 0 eller 1 |
| Det forudsagte output er en kontinuerlig variabel | Den forudsagte output er en diskret variabel |
| Forudsagt output Y kan overstige 0 og 1 område | Forudsagt output Y ligger inden for 0 og 1 område |
 | 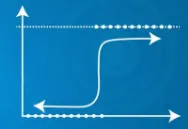 |
| Forudsagt output Y kan overstige 0 og 1 område | Forudsagt output |
Konklusion
Hvis funktioner ikke bidrager til forudsigelse, eller hvis de er meget korrelerede med hinanden, tilføjer det støj til modellen. Funktioner, der ikke bidrager nok til modellen, skal fjernes. Hvis uafhængige variabler er meget korrelerede, kan det forårsage et problem med multikollinearitet, som kan løses ved at køre separate modeller med hver uafhængig variabel.
Anbefalede artikler
Dette har været en guide til Lineær Regression vs Logistic Regression. Her diskuterer vi Linear Regression vs Logistic Regression nøgleforskelle med infografik og sammenligningstabel. Du kan også se på de følgende artikler for at lære mere–
- Data Science vs Data Visualization
- Machine Learning vs Neural Network
- Overvåget læring vs dyb læring
- Logistisk regression i R