
Introduktion til DFS-algoritme
DFS er kendt som Depth First Search Algorithm, der giver trinnene til at krydse hver knude på en graf uden at gentage nogen knude. Denne algoritme er den samme som Depth First Traversal for et træ, men adskiller sig fra at opretholde en boolsk for at kontrollere, om noden allerede er besøgt eller ikke. Dette er vigtigt for grafovergang, da der også findes cykler i grafen. En bunke opretholdes i denne algoritme til lagring af de suspenderede knudepunkter, mens de gennemgår. Det hedder det, fordi vi først rejser til dybden af hver tilstødende knude og derefter fortsætter med at krydse en anden tilstødende knude.
Forklar DFS-algoritmen
Denne algoritme er i modsætning til BFS-algoritmen, hvor alle de tilstødende knudepunkter besøges, efterfulgt af naboer til de tilstødende knudepunkter. Det begynder at udforske grafen fra en knude og udforske dens dybde før backtracking. To ting overvejes i denne algoritme:
- Besøg i en toppunkt : Valg af en toppunkt eller knude på grafen for at krydse.
- Undersøgelse af en toppunkt : Gennemse alle noder, der støder op til det toppunkt.
Pseudokode for dybde Første søgning :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Linear Traversal findes også for DFS, der kan implementeres på 3 måder:
- Forudbestille
- Med sigte
- Postorder
Omvendt postorder er en meget nyttig måde at krydse og bruges til topologisk sortering samt forskellige analyser. Der opretholdes også en stabel til opbevaring af de knudepunkter, hvis efterforskning stadig venter.
Graf Traverse i DFS
I DFS følges nedenstående trin for at krydse grafen. For eksempel, en given graf, lad os starte gennemgang fra 1:
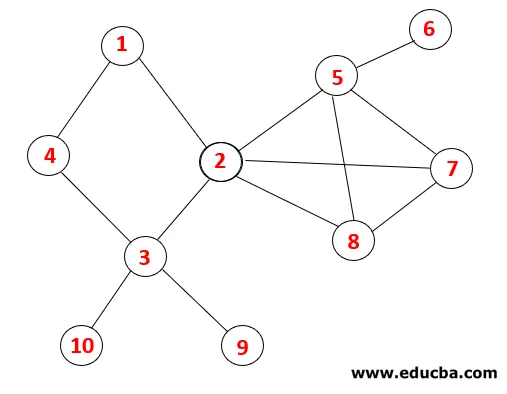
| Stak | Traversalsekvens | Spændende træ |
| 1 |  |
|
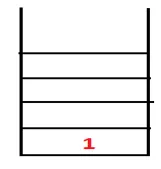 | 1, 4 |  |
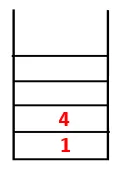 | 1, 4, 3 |  |
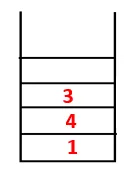 | 1, 4, 3, 10 | 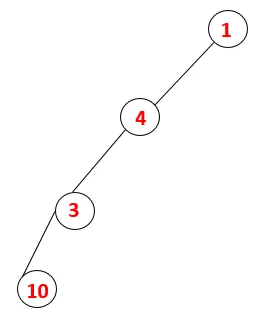 |
 | 1, 4, 3, 10, 9 | 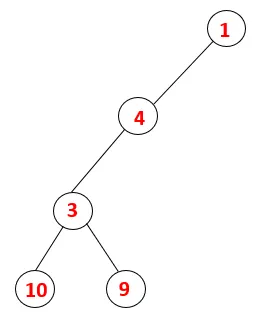 |
 | 1, 4, 3, 10, 9, 2 | 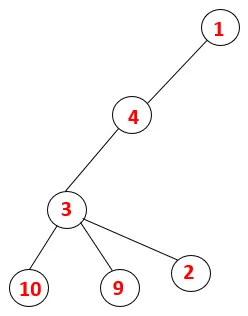 |
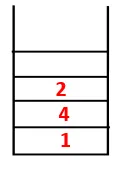 | 1, 4, 3, 10, 9, 2, 8 |  |
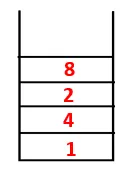 | 1, 4, 3, 10, 9, 2, 8, 7 | 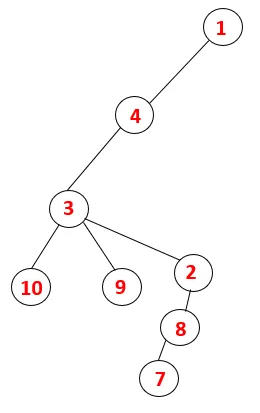 |
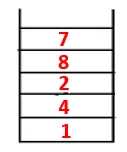 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
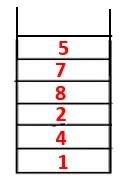 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 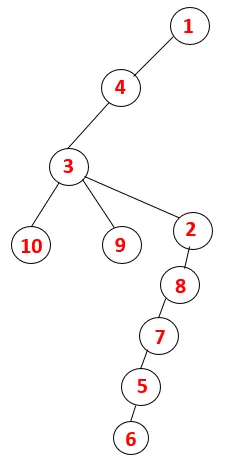 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 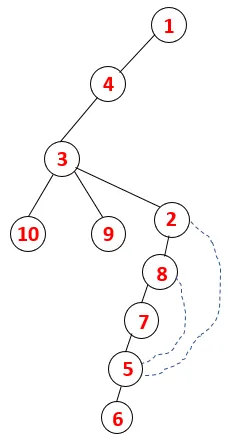 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
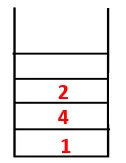 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 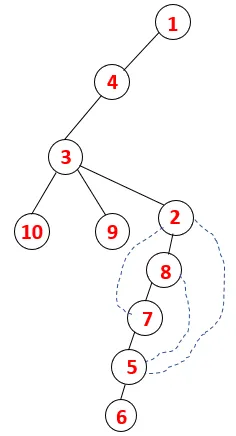 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 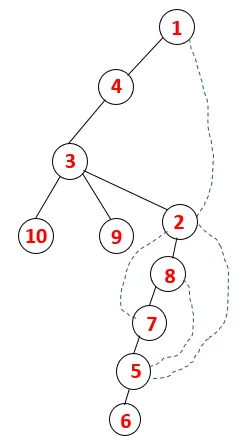 |
Forklaring til DFS-algoritme
Nedenfor er trinnene til DFS-algoritme med fordele og ulemper:
Trin 1: Node 1 besøges og tilføjes til sekvensen såvel som det spændende træ.
Trin 2: Tilgrænsende noder fra 1 udforskes, som er 4, således at 1 skubbes til stakken og 4 skubbes ind i sekvensen såvel som spændende træ.
Trin 3: En af de tilstødende knudepunkter på 4 udforskes, og 4 skubbes således til stakken, og 3 går ind i sekvensen og det spændende træ.
Trin 4: Tilgrænsende knudepunkter af 3 udforskes ved at skubbe den ind på stakken og 10 går ind i sekvensen. Da der ikke er nogen tilstødende knude til 10, springes derved 3 ud af stakken.
Trin 5: En anden tilstødende knude af 3 udforskes og 3 skubbes ind på stakken og 9 besøges. Intet tilstødende knudepunkt på 9 således 3 poppes ud, og den sidste tilstødende knude på 3 dvs. 2 besøges.
En lignende proces følges for alle knudepunkter, indtil stakken bliver tom, hvilket indikerer stopbetingelsen for gennemgangsalgoritmen. - -> stiplede linjer i det spændende træ henviser til bagkanterne, der findes i grafen.
På denne måde kører alle knudepunkter i grafen uden at gentage nogen af knudepunkterne.
Fordele og ulemper
- Fordele: Denne hukommelseskrav til denne algoritme er meget mindre. Mindre rum og tidskompleksitet end BFS.
- Ulemper: Løsning er ikke garanteret Programmer. Topologisk sortering. Find grafbroer.
Eksempel til implementering af DFS-algoritme
Nedenfor er eksemplet til implementering af DFS-algoritme:
Kode:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Produktion:
Forklaring til ovenstående program: Vi lavede en graf med 5 vertikater (0, 1, 2, 3, 4) og brugte besøgte array for at holde styr på alle besøgte hjørner. Derefter gentages for hver knude, hvis tilstødende knudepunkter, den samme algoritme, indtil alle noder er besøgt. Derefter går algoritmen tilbage til at ringe til toppunkt og poppe den fra stakken.
Konklusion
Hukommelsesbehovet i denne graf er mindre sammenlignet med BFS, da der kun er behov for en bunke for at opretholdes. Et DFS-spændende træ og en gennemgående sekvens genereres som et resultat, men er ikke konstant. Flere traversalsekvenser er mulige, afhængigt af det valgte startpunkt og det valgte efterforskningspunkt.
Anbefalede artikler
Dette er en guide til DFS-algoritme. Her diskuterer vi trinvis forklaring, krydse grafen i et tabelformat med fordele og ulemper. Du kan også gennemgå vores andre relaterede artikler for at lære mere -
- Hvad er HDFS?
- Deep Learning Algorithms
- HDFS-kommandoer
- SHA-algoritme