
Variationskoefficientformel (indholdsfortegnelse)
- Formel
- eksempler
Hvad er variationskoefficientformlen?
I statistikker er variationskoefficienten også kaldet CV et værktøj, der hjælper os med at bestemme, hvordan datapunkter i et datasæt er fordelt omkring middelværdien. Grundlæggende er alle datapunkter plottet først, og derefter bruges variationskoefficienten til at måle spredningen af disse punkter fra hinanden og middelværdien. Så det hjælper os med at forstå dataene og også se det mønster, de danner. Det beregnes som et forhold mellem standardafvigelsen for datasættet og middelværdien. Højere variationskoefficient betyder, at der er et større niveau for spredning af data omkring middelværdien. På lignende måde, lavere værdien af variationskoefficienten, mindre er spredningen og mere præcise vil resultaterne være. Selv hvis middelværdien af to dataserier er betydeligt forskellige, er variationskoefficienten meget nyttig til at sammenligne variationen i graden fra den ene dataserie til den anden.
Formel for variationskoefficient er givet af:
Coefficient of Variation = Standard Deviation / Mean
Trin til beregning af variationskoefficient:
Trin 1: Beregn gennemsnittet af datasættet. Middelværdien er gennemsnittet af alle værdier og kan beregnes ved at tage summen af alle værdierne og derefter dele det med et antal datapunkter.
Trin 2: Beregn derefter standardafvigelsen for datasættet. Det er en lidt tidskrævende proces. Standardafvigelse kan beregnes som: √ (Σ (X i - X m ) 2 / (n - 1)) . Xi er det ith datapunkt, og X m er gennemsnittet af datasættet. Alternativt kan vi også finde standardafvigelsen i Excel ved hjælp af funktionen STDEV.S ().
Trin 3: Del standardafvigelse med middel for at få variationskoefficienten.
Eksempler på variationskoefficientformel (med Excel-skabelon)
Lad os tage et eksempel for at forstå beregningen af variationskoefficienten på en bedre måde.
Du kan downloade denne Koefficient of Variation Formula Excel Template here - Coefficient of Variation Formula Excel TemplateVariationskoefficientformel - eksempel # 1
Lad os sige, at vi har to datasæt A & B, og hver indeholder 20 tilfældige datapunkter. Beregn variationskoefficienten for datasættet X & Y.
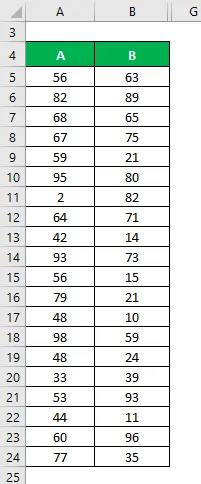
Løsning:
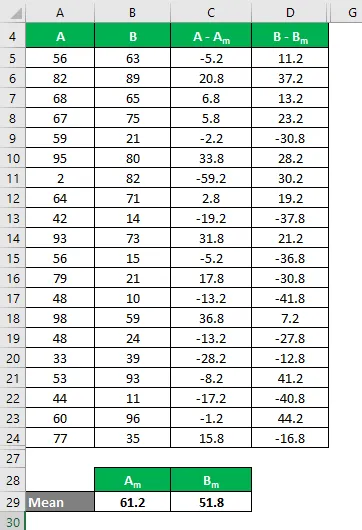
Gennemsnit beregnes som:
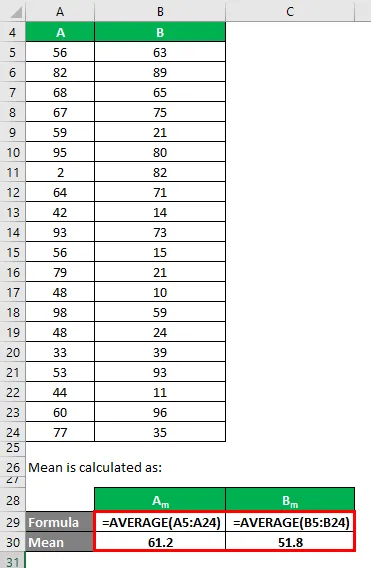
- Gennemsnit af datasæt A = 61.2
- Gennemsnit af datasæt B = 51, 8
Nu skal vi beregne forskellen mellem datapunkter og middelværdien.
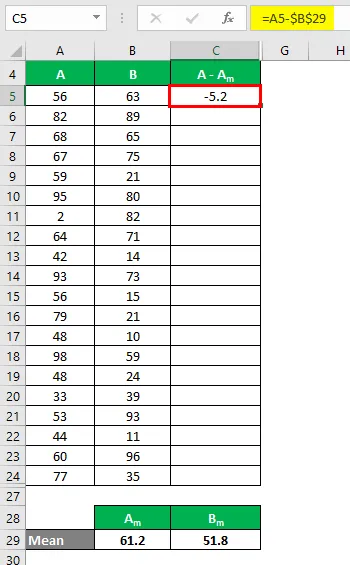
Beregn ligeledes for alle værdier i datasættet A.
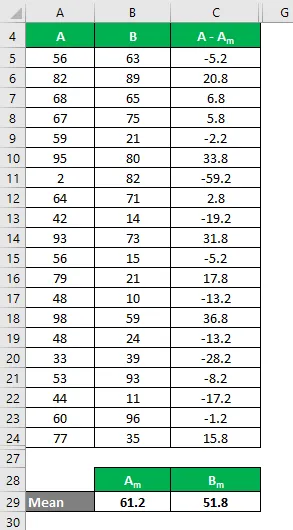
Beregn ligeledes for alle værdier i datasættet B.
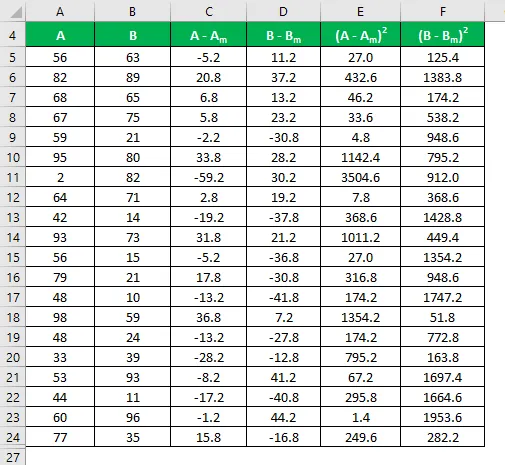
Beregn kvadratet af forskellen for både datasættene A og B.
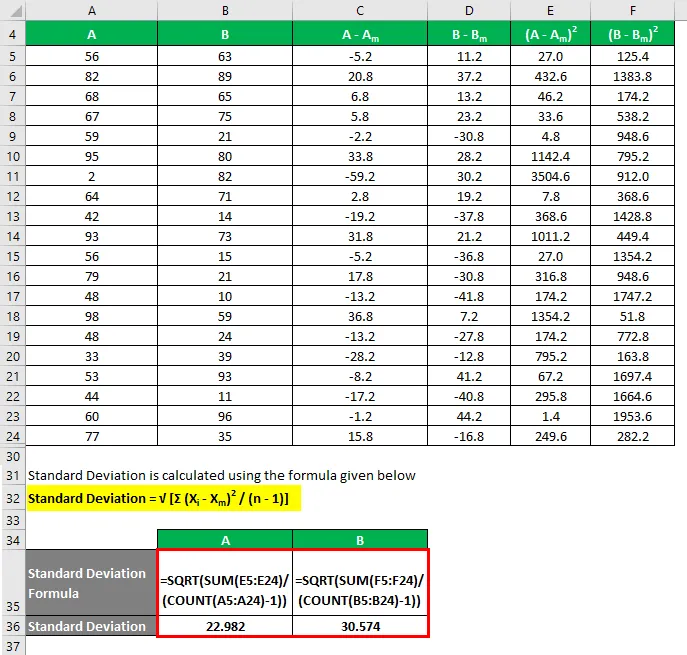
Standardafvigelse beregnes ved hjælp af nedenstående formel
Standardafvigelse = √ (Σ (X i - X m ) 2 / (n - 1))
Variationskoefficient beregnes ved hjælp af nedenstående formel
Variationskoefficient = Standardafvigelse / middelværdi
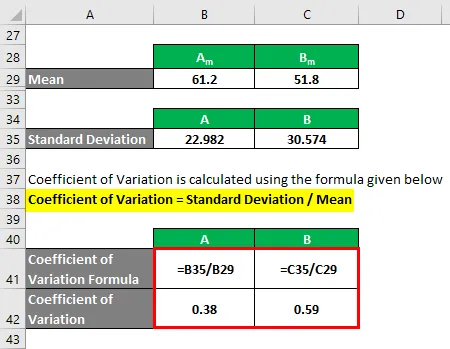
- Variationskoefficient A = 22.982 / 61.2 = 0.38
- Variationskoefficient B = 30, 574 / 51, 8 = 0, 59
Så hvis du ser her, har B en højere variationskoefficient end A, hvilket betyder, at datapunkter for B er mere spredt end A.
Variationskoefficientformel - eksempel # 2
Lad os sige, at du er en meget risikovillig investor, og du ønsker at investere penge på aktiemarkedet. Da din risikoappetit er lav, vil du investere i sikre lagre, der har lavere standardafvigelse og variationskoefficient. Du har valgt 3 aktier på baggrund af deres grundlæggende og tekniske oplysninger og vil vælge 2 aktier. Du har også samlet oplysninger om deres historiske afkast i de sidste 15 år.
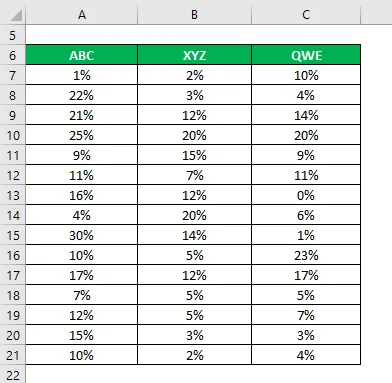
Løsning:
Gennemsnit beregnes som:
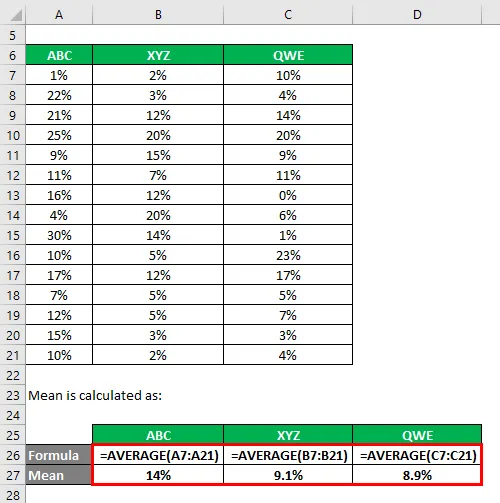
Standardafvigelse beregnes ved hjælp af excelformel
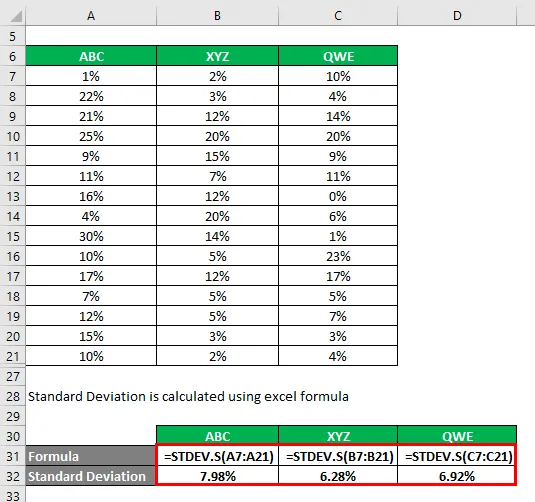
Variationskoefficient beregnes ved hjælp af nedenstående formel
Variationskoefficient = Standardafvigelse / middelværdi
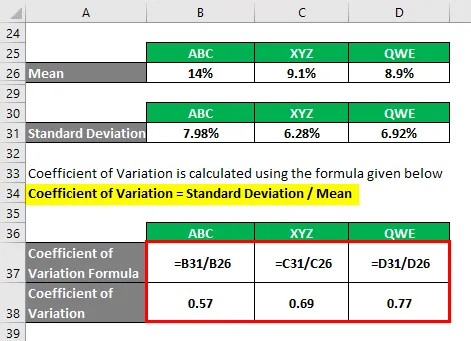
- Variationskoefficient ABC = 7, 98% / 14% = 0, 57
- Variationskoefficient XYZ = 6, 28% / 9, 1% = 0, 69
- Variationskoefficient QWE = 6, 92% / 8, 9% = 0, 77
Baseret på oplysningerne vælger du aktie ABC og XYZ at investere, da de har den laveste variationskoefficient.
Forklaring
Da variationskoefficienten er et mål for risiko, hjælper det med at måle volatiliteten i priserne på aktier og andre finansielle instrumenter. Det hjælper også investorer og analytikere med at sammenligne de risici, der er forbundet med forskellige potentielle investeringer.
Variationskoefficient ligner standardafvigelse, men en standardafvigelse for to variabler kan ikke sammenlignes med brugbarhed. Men ved at bruge standardafvigelse og middelværdien gør den relative sammenligning mere meningsfuld. Der er også en begrænsning af variationskoefficienten. Antag, at gennemsnittet af et datasæt er nul. I dette tilfælde vil dette værktøj blive ineffektivt. Ikke kun dette, hvis vi har et datasæt, der har mange positive og negative værdier, bliver variationskoefficienten meget problematisk. Så det er kun mere nyttigt med datasæt, der har det samme plus-minus-tegn.
Relevans og anvendelser af variationskoefficientformel
Variationskoefficient har relevans inden for mange andre områder end statistik. For eksempel inden for finansiering er variationskoefficienten et mål for risiko. Det ligner standardafvigelse, da det også bruges som et mål for risiko, men forskellen er, at variationskoefficienten er en bedre indikator for relativ risiko. Lad os f.eks. Sige, at A's forventede afkast på 15% og B's forventede afkast på 10% og A har en standardafvigelse på 10%, mens B har en standardafvigelse på 5%. For at vælge en bedre investering kan variationskoefficienten bruges. Så variationskoefficienten for A er 10/15 = 0, 666, og variationskoefficienten for B er 5/10 = 0, 5. Så B er en bedre investering end A.
Anbefalede artikler
Dette har været en guide til formel for koefficient af variation. Her diskuterer vi, hvordan man beregner variationskoefficienten ved hjælp af formel sammen med praktiske eksempler og downloadbar excel-skabelon. Du kan også se på de følgende artikler for at lære mere -
- Hvad er Justeret R-kvadratformel?
- Eksempler på koefficient for bestemmelsesformel
- Hvordan beregnes korrelationskoefficienten ved hjælp af formler?
- Covariance-formel med Excel-skabelon