Effektiv årlig kursformel (indholdsfortegnelse)
- Formel
- eksempler
- Lommeregner
Hvad er den effektive årlige kursformel?
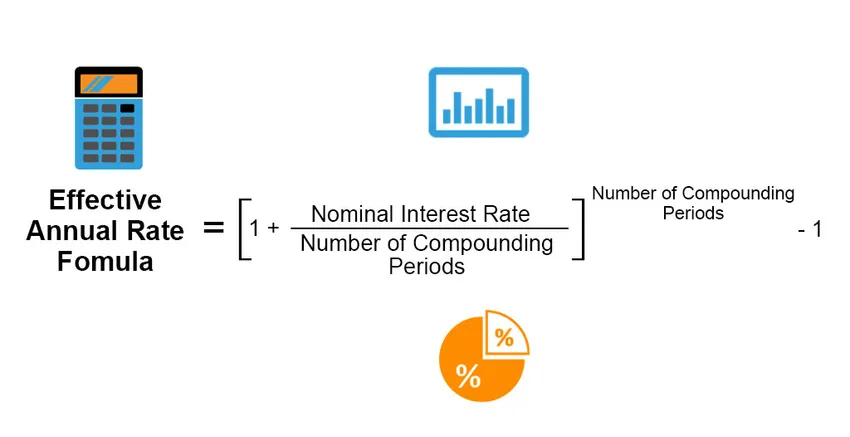
Effektiv årlig rente er den faktiske rentesats, der optjenes eller udbetales på en investering, et lån eller et lignende finansielt produkt, og den er ellers forskellig fra "nominel rente" på grund af udbetalingsperioden for renter, sammensætning af rente, samlet lånets eller investeringens tidsperiode osv. Den effektive årlige sats beregnes med følgende formel;
Effective Annual Rate = ((1 + (Nominal Interest Rate / Number of Compounding Periods)) Number of Compounding Periods) – 1
Eksempler på effektiv årlig rateformel (med Excel-skabelon)
Lad os tage et eksempel for at forstå beregningen af effektiv årlig rente på en bedre måde.
Du kan downloade denne effektive årlige satsformel Excel-skabelon her - Effektiv årlig satsformel Excel-skabelonEffektiv årlig kursformel - eksempel # 1
Antag, at en Mr. X optager et personligt lån fra en bank med en rente på 20%, sammensat halvårligt. Beregn effektiv årlig sats ved hjælp af oplysningerne.

Løsning:
Den effektive årlige sats beregnes ved hjælp af nedenstående formel
Effektiv årlig sats = ((1 + (nominel rente / antal sammensatte perioder)) Antal sammensatte perioder) - 1

- Effektiv årlig sats = ((1 + (20% / 2)) 2) - 1
- Effektiv årlig sats = 21%
Effektiv årlig kursformel - eksempel # 2
Antag, at Mr. A investerede $ 100 i et indskudsbevis, der udbetaler en nominel årlig rente på 10% sammensat på kvartalsbasis. Beregn den effektive årlige sats.

Løsning:
Den effektive årlige sats beregnes ved hjælp af nedenstående formel
Effektiv årlig sats = ((1 + (nominel rente / antal sammensatte perioder)) Antal sammensatte perioder) - 1
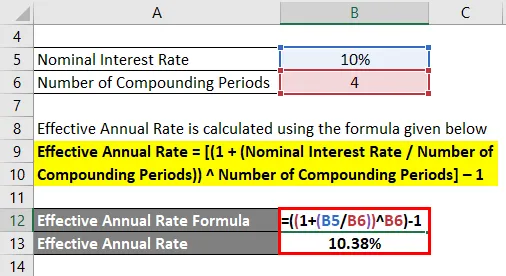
- Effektiv årlig sats = ((1 + (10% / 4)) 4) - 1
- Effektiv årlig sats = 10, 38%
Effektiv årlig kursformel - eksempel # 3
Lad os antage, at investeringer i gensidige fonde henter 15, 50% årlig rente som indtjening, mens P2P-udlån tjener 15% årlig nominel rente, sammensat månedligt. Så beregn den effektive årlige sats for begge tilfælde.

Løsning:
Den effektive årlige sats beregnes ved hjælp af nedenstående formel
Effektiv årlig sats = ((1 + (nominel rente / antal sammensatte perioder)) Antal sammensatte perioder) - 1
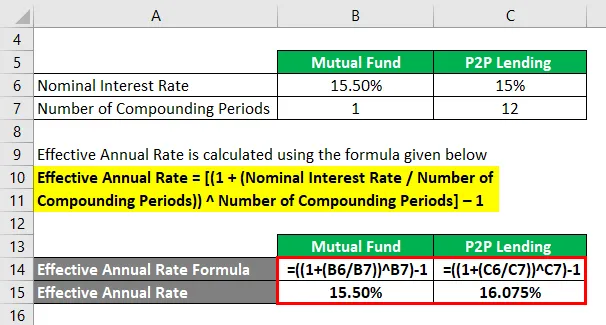
For gensidig fond
- Effektiv årlig sats = ((1 + (15, 50% / 1)) 1) - 1
- Effektiv årlig sats = 15, 50%
Til P2P-udlån
- Effektiv årlig sats = ((1 + (15% / 12)) 12) - 1
- Effektiv årlig sats = 16, 075%
Forklaring
Den nominelle rente er den angivne rente på det finansielle produkt. I eksempel 3 får den nominelle kurs, der vises på produkterne, den gensidige fond til at ligne det foretrukne valg af investering for investorer på grund af den 0, 50% højere årlige nominelle rente, der er optjent.
Den effektive årlige rente beregnes imidlertid ved at tage den nominelle årlige rente og sammensætte den for antallet af specificerede perioder (12 hvis sammensætning er månedlig; 6 hvis sammensætning er to-månedlig; 4 hvis den er kvartalsvis og 2 hvis den er halvårlig) gældende i et tidsrum på et år. I tilfælde af gensidig fond er antallet af sammensatte perioder pr. År 1, mens det i tilfælde af P2P-udlån er den månedlige sammensætning, hvorfor der er 12 sammensatte perioder.
Baseret på formlen,
Effektivt årligt afkast = ((1 + (nominel rente / antal sammensatte perioder)) (antal sammensatte perioder)) - 1
Gensidig fonds effektiv årlig afkast = ((1 + (15, 50% / 1)) 1) - 1 = 15, 50%
P2P-udlån Effektiv årlig afkast = ((1 + (15, 00% / 12)) 12) - 1 = 16, 075%
Relevans og anvendelser af effektiv årlig satsformel
Den effektive årlige renteformel bruges til at skelne mellem den faktiske IRR (Intern afkast) eller et årligt udbytte for en rente, der måske måske ikke blandes flere gange over en given periode. Dette kan meget vel bruges til at sammenligne forskellige slags investeringsmuligheder eller lånefaciliteter taget under forskellige strukturer.
Lad os antage, at der er 2 investeringsmuligheder, postkontortidindskud og faste bankindskud, som en investor er indsnævret til, i betragtning af hans / hendes risikovilje og egnethed. Investorens ultimative mål er at få mest muligt ud af disse indskud og tjene et højere afkast. Begge instrumenter tilbyder dog lidt forskellige renter, mens Post Office Term Deposit tilbyder kvartalsvis sammensætning for den betragtede periode.
- Investeringsbeløb: Rs. 10 lakhs
- Investeringsperiode: 5 år
- Bankindskud: 7, 5% årlig rente
- Depositum for postkontor: 7, 4% årlig rente, sammensat kvartalsvis
Ved at se de årlige renter, der ser ud, ser det ud til, at den faste bankindskud er den bedre mulighed. Hvis investoren imidlertid faktisk beregner den kvartalsvise sammensætningsfaktor for Post Office Term Depositum, resulterer det i en effektiv årlig rente / afkast på 7, 61%.
På grund af denne lille ændring fra 7, 4% til 7, 61% i effektiv rente, ville investoren tjene i alt Rs. 4.42.848, 28 fra dette instrument, hvorimod han / hun ville have tjent Rs. 3, 35.469, 14 fra bankens faste indbetalingsinstrument.
Hvis investoren går glip af beregningen af denne effektive årlige rente, ville han / hun have mistet muligheden for at opnå cirka mere end Rs. 1 lakh fra hans investering.
Effektiv beregning af den årlige kursformel
Du kan bruge følgende effektive årlige kursberegner
| Nominel rente | |
| Antal forbindelsesperioder | |
| Effektiv årlig sats | |
| Effektiv årlig sats = | ((1 + (nominel rente / antal sammensatte perioder)) Antal forbindelsesperioder ) - 1 | |
| ((1 + (0/0)) 0 ) - 1 = | 0 |
Anbefalede artikler
Dette er en guide til effektiv årlig kursformel. Her diskuterer vi Sådan beregnes effektiv årlig sats sammen med praktiske eksempler. Vi leverer også en effektiv årlig kursberegner med downloadbar excel-skabelon. Du kan også se på de følgende artikler for at lære mere -
- Lommeregner til formel for real rente
- Afkast på kapital beskæftiget formel | Definition
- Hvordan beregnes den effektive rentesats?
- Hvad er nutidsværdien af annuitetsformlen?