
Introduktion til Hashing-funktion i C
Denne artikel har en kort note om hashing (hash-tabel og hash-funktion). Det vigtigste koncept er 'søgning', der bestemmer tidskompleksiteten. For at reducere tidskompleksiteten end nogen anden datastruktur introduceres hashing-koncept, der har O (1) tid i gennemsnit, og i værste tilfælde vil det tage O (n) tid.
Hashing er en teknik med hurtigere adgang til elementer, der kortlægger de givne data med en mindre nøgle til sammenligning. Generelt i denne teknik spores nøglerne ved hjælp af hash-funktion til en tabel kendt som hash-tabellen.
Hvad er Hash-funktion?
Hash-funktionen er en funktion, der bruger konstant-tid-operationen til at gemme og hente værdien fra hash-tabellen, der anvendes på tasterne som heltal, og denne bruges som adresse til værdier i hash-tabellen.
Typer af en Hash-funktion
Typerne af hashfunktioner er forklaret nedenfor:
1. Opdelingsmetode
I denne metode er hash-funktionen afhængig af resten af en opdeling.
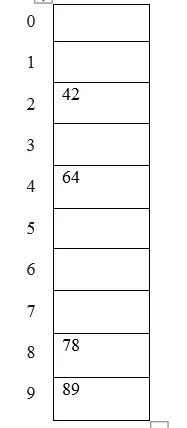
Eksempel: elementer, der skal placeres i en hash-tabel er 42, 78, 89, 64, og lad os tage bordstørrelse som 10.
Hash (nøgle) = Elementer% tabelstørrelse;
2 = 42% 10;
8 = 78% 10;
9 = 89% 10;
4 = 64% 10;
Tabellrepræsentationen kan ses som nedenfor:
2. Mid firkantet metode
I denne metode tages den midterste del af det firkantede element som indekset.
Element, der skal placeres i hashbordet er 210, 350, 99, 890 og størrelsen på bordet er 100.
210 * 210 = 44100, indeks = 1 som den midterste del af resultatet (44100) er 1.
350 * 350 = 122500, indeks = 25 som den midterste del af resultatet (122500) er 25.
99 * 99 = 9801, indeks = 80 som den midterste del af resultatet (9801) er 80.
890 * 890 = 792100, indeks = 21 som den midterste del af resultatet (792100) er 21.
3. Digit foldemetode
I denne metode er det element, der skal placeres i tabellen uh, sing hash-nøglen, som opnås ved at dele elementerne i forskellige dele og derefter kombinere delene ved at udføre nogle enkle matematiske operationer.
Element, der skal placeres, er 23576623, 34687734.
- hash (nøgle) = 235 + 766 + 23 = 1024
- hash-nøgle) = 34 + 68 + 77 + 34 = 213
I disse typer hashing antager vi, at vi har tal fra 1- 100 og størrelsen på hash-tabel = 10. Elementer = 23, 12, 32
Hash (nøgle) = 23% 10 = 3;
Hash (nøgle) = 12% 10 = 2;
Hash (nøgle) = 32% 10 = 2;
Fra ovenstående eksempel skal du bemærke, at begge elementer 12 og 32 peger på 2. plads i tabellen, hvor det ikke er muligt at skrive begge på samme sted, et sådant problem er kendt som en kollision. For at undgå denne form for problemer er der nogle teknikker med hashfunktioner, der kan bruges.
Typer af kollisionsopløsningsteknikker
Lad os diskutere typerne af kollisionsopløsningsmetoder:
1. Kæde
I denne metode, som navnet antyder, giver den en kæde med kasser til posten i tabellen med to poster af elementer. Så når sådanne kollisioner opstår, fungerer kasserne som en sammenkoblet liste.
Eksempel: 23, 12, 32 med bordstørrelse 10.
Hash (nøgle) = 23% 10 = 3;
Hash (nøgle) = 12% 10 = 2;
Hash (nøgle) = 32% 10 = 2;
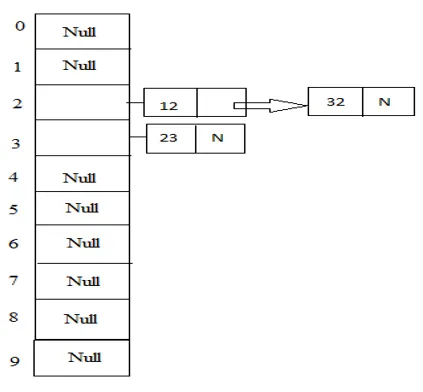
2. Åbn adressering
- Lineær sondering
Dette er en anden metode til løsning af kollisionsproblemer. Som navnet siger, hver gang en kollision opstår, skal to elementer placeres på den samme post i tabellen, men ved hjælp af denne metode kan vi søge efter næste tom plads eller post i tabellen og placere det andet element. Dette kan igen føre til et andet problem; hvis vi ikke finder nogen tom post i tabellen, fører det til klynger. Dette er således kendt som et klyngeproblem, som kan løses ved følgende metode.
Eksempel: 23, 12, 32 med bordstørrelse 10
Hash (nøgle) = 23% 10 = 3;
Hash (nøgle) = 12% 10 = 2;
Hash (nøgle) = 32% 10 = 2;

I dette diagram kan 12 og 32 placeres i samme indgang med indeks 2, men ved denne metode er de placeret lineært.
- Kvadratisk sondering
Denne metode er en opløsning til klyngeproblemet under lineær sondering. I denne metode beregnes hash-funktionen med hash-nøglen som hash (nøgle) = (hash (nøgle) + x * x)% af tabellens størrelse (hvor x = 0, 1, 2 …).
Eksempel: 23, 12, 32 med bordstørrelse 10
Hash (nøgle) = 23% 10 = 3;
Hash (nøgle) = 12% 10 = 2;
Hash (nøgle) = 32% 10 = 2;

I dette kan vi se, at 23 og 12 let kan placeres, men 32 kan ikke igen 12 og 32 deler den samme post med samme indeks i tabellen, som pr. Denne metode hash (nøgle) = (32 + 1 * 1) % 10 = 3. Men i dette tilfælde er indtastning af tabel med indeks 3 placeret med 23, så vi er nødt til at øge x-værdien med 1. Hash (nøgle) = (32 + 2 * 2)% 10 = 6. Så vi kan nu placere 32 i posten med indeks 6 i tabellen.
- Dobbelt hashing
Denne metode skal vi beregne 2 hash-funktioner for at løse kollisionsproblemet. Den første beregnes ved hjælp af en enkel opdelingsmetode. For det andet skal to regler overholdes; det må ikke være lig med 0, og poster skal efterforskes.
- 1 (nøgle) = nøgle% størrelse på tabellen.
- 2 (nøgle) = p - (nøglemod p), hvor p er primtal <tabellens størrelse.
Eksempel: 23, 12, 32 med bordstørrelse 10
Hash (nøgle) = 23% 10 = 3;
Hash (nøgle) = 12% 10 = 2;
Hash (nøgle) = 32% 10 = 2;
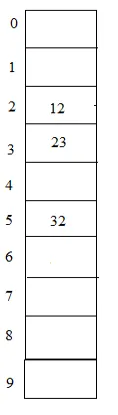
I dette igen kan elementet 32 placeres ved hjælp af hash2 (nøgle) = 5 - (32% 5) = 3. Så 32 kan placeres ved indeks 5 i tabellen, som er tom, da vi er nødt til at hoppe 3 poster for at placere det.
Konklusion-Hashing-funktion i C
Hashing er en af de vigtige teknikker med hensyn til søgning af data forsynet med meget effektive og hurtige metoder ved hjælp af hash-funktion og hash-tabeller. Hvert element kan søges og placeres ved hjælp af forskellige hashmetoder. Denne teknik er meget hurtigere end nogen anden datastruktur med hensyn til tidskoefficient.
Anbefalede artikler
Dette er en guide til Hashing-funktionen i C. Her diskuterer vi introduktionen af Hashing-funktionen i C, Hvad er Hash-funktion, typer af en hash-funktion osv. Du kan også gennemgå vores andre foreslåede artikler for at lære mere–
- Hashing i DBMS
- Krypteringsproces
- Sådan installeres CakePHP?
- Sådan fungerer Blockchain
- Hashing-funktion i Java
- Hashing-funktion i PHP | Hvordan man arbejder?