
Introduktion til eksempler på standardafvigelse
Der er rigelige eksempler på standardafvigelser. Standardafvigelse er målet for spredning af datasæt, dvs. hvor spredt tallene er. Det er nyttigt at sammenligne de forskellige datasæt, der kan have samme gennemsnit men det forskellige interval. Følgende forskellige standardafvigelseseksempel giver forståelse for den mest almindelige type situationer, hvor standardafvigelsen beregnes, og hvordan man kan beregne det samme
Eksempler på standardafvigelse
Nedenfor er eksemplerne på standardafvigelsen
Standardafvigelse - eksempel # 1
Aktien i Company Z sælger for $ 50 pr. Aktie og de samme tilbud efter udbetalinger for det næste år:
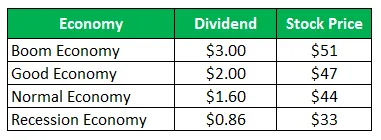
Beregn standardafvigelsen, når alle de fire scenarier er givet, er lige sandsynlige.
Løsning:
Beregninger af tilbageholdelsesperiode (HPR) er som følger -
Formel af HPR
HPR = ((Periodens slutværdi - Originalværdi) + Indkomst) / Originalværdi) * 100
For Boom Economy
- HPR (boom) = ((51-50) + 3) / 50 = 8, 00%
- HPR (god) = ((47-50) + 2) / 50 = -2, 00%
- HPR (Normal) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (recession) = ((33-50) + 0, 86) / 50 = -32, 28%
Beregning af forventet afkast
Da alle scenarier er lige sandsynlige, vil sandsynligheden for alle være ¼
Formel for forventet afkast
Forventet retur = (sandsynlighed for bom * retur fra bom) + (sandsynlighed for god * tilbagevenden fra god) + (sandsynlighed for normal * retur fra normal) + (sandsynlighed for recession * retur fra recession)
- Forventet afkast = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Forventet afkast = -8, 77%
Beregning af standardafvigelse
Formel for variation
Variance = (Sandsynlighed for bom * (Return from Boom - Total Expected Return) 2) + (Probability of Good * (Return from Good - Total Expected Return) 2) + (Sandsynlighed for Normal * (Return from Normal - Total Expected Return) 2 ) + (Sandsynlighed for recession * (Return from Recession –Total Expected Return) 2)
- Varians = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Varians = 219, 95
Formel for standardafvigelse
Standardafvigelse vil være firkantet rod af variation
Standardafvigelse = √Variance
- Standardafvigelse = √ 219, 95
- Standardafvigelse = 14, 83%
Standardafvigelseseksempel - 2
Standardafvigelse for to selskaber i porteføljen
Selskabets fælles aktie sælger for $ 28 pr. Aktie og de samme tilbud efter udbetalinger for det næste år

Den fælles aktie i virksomhed B sælger for $ 93 pr. Aktie og de samme tilbud efter udbetalinger for det næste år:

(a) Beregn standardafvigelsen for virksomhed A
(b) Beregn standardafvigelsen for virksomhed B
(c) Beregn porteføljens standardafvigelse, hvis halvdelen af investeringen foretages er virksomhed A og resten halvdelen i virksomhed B
Løsning:
For firma A
Beregninger af afholdelse af tilbageholdelsesperiode (HPR)
Formel af HPR
HPR = ((Periodens slutværdi - Originalværdi) + Indkomst) / Originalværdi) * 100
- HPR (bom) = ((20-28) + 1) / 28 = -25, 00%
- HPR (Normal) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (recession) = ((38-28) + 5) / 28 = 53, 57%
Beregning af forventet afkast af virksomhed A
Formel for forventet afkast
Forventet retur = (sandsynlighed for bom * retur fra bom) + (sandsynlighed for normal * tilbagevenden fra normal) + (sandsynlighed for recession * retur fra recession)
- Forventet afkast = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Forventet afkast = 3, 84%
Beregning af standardafvigelsesfirma A
Formel for variation
Variance = (Sandsynlighed for bom * (Return from Boom - Total Expected Return) 2) + (Probability of Normal * (Return from Normal - Total Expected Return) 2 ) + (Probabilitet for recession * (Return from Recession - Total Expected Return) 2)
- Varians = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Varians = 895, 15
Formel for standardafvigelse
Standardafvigelse vil være firkantet rod af variation
Standardafvigelse = √Variance
- Standardafvigelse = √ 895.15
- Standardafvigelse = 29, 92%
For firma B
Beregninger af tilbageholdelse af periode (HPR)
Formel af HPR
HPR = ((Periodens slutværdi - Originalværdi) + Indkomst) / Originalværdi) * 100
HPR (Boom) = ((200-93) +7) / 93 = 122, 58%
HPR (Normal) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (recession) = ((4-93) +2) / 93 = -93, 55%
Beregning af forventet afkast
Formel for forventet afkast
Forventet retur = (sandsynlighed for bom * retur fra bom) + (sandsynlighed for normal * tilbagevenden fra normal) + (sandsynlighed for recession * retur fra recession)
- Forventet afkast = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Forventet afkast = 43, 04%
Beregning af standardafvigelse
Formel for variation
Variance = (Sandsynlighed for bom * (Return from Boom - Total Expected Return) 2) + (Probability of Normal * (Return from Normal - Total Expected Return) 2 ) + (Probabilitet for recession * (Return from Recession - Total Expected Return) 2)
- Varians = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Varians = 6783, 65
Formel for standardafvigelse
Standardafvigelse vil være firkantet rod af variation
Standardafvigelse = √Variance
- Standardafvigelse = √6783.65
- Standardafvigelse = 82, 36%
Beregning af forventet afkast og standardafvigelse for en porteføljehalvdel investeret i selskab A og halvdel i selskab B.
Standardafvigelse for virksomhed A = 29, 92%
Standardafvigelse for virksomhed B = 82, 36%
Firmaets vægt = 0, 50
Virksomhed B's vægt = 0, 50
Formlen for standardafvigelse for portefølje
Standardafvigelse af portefølje = (Vægt af selskab A * Forventet afkast af selskab A) + ((vægt på selskab B * forventet afkast af selskab B)
- Standardafvigelse for portefølje = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Standardafvigelse for portefølje = 56, 14%
Analyse
Porteføljens standardafvigelse er lavere end for begge aktiers individuelle, fordi lagrene er diversificeret i forskellige aktier. Diversificering fører til en reduktion i risikoen, medmindre der er en perfekt sammenhæng mellem afkast på porteføljeinvesteringer.
Konklusion - eksempler på standardafvigelse
Standardafvigelsen måler spredningen af datasættet, der er i forhold til dets gennemsnit. Det beregnes som kvadratroten af varians. Jo større standardafvigelsen for sikkerheden er, jo større vil variationen mellem hver pris og middelværdi være, hvilket viser, at prisintervallet er stort. Ovennævnte eksempler er nogle af eksemplerne på standardafvigelse på forskellige måder. Der er også forskellige andre eksempler, der viser, at standardafvigelse kan beregnes ved hjælp af andre data.
Anbefalede artikler
Dette har været en guide til standardafvigelseseksemplerne. Her diskuterer vi de forskellige eksempler på standardafvigelse sammen med en detaljeret forklaring . Du kan også se på de følgende artikler for at lære mere -
- Eksempel på faste omkostninger
- Variabel omkostningseksempel
- Kvantitativt eksempel
- Eksempler på monopolistisk konkurrence