Nuværdiformel - Lommeregner (eksempler med Excel-skabelon)

Nuværende værdiformel (indholdsfortegnelse)

• Formel
• eksempler
• Lommeregner

Hvad er den nuværende værdiformel?

Udtrykket "nutidsværdi" henviser til anvendelsen af ​​tidsværdien af ​​penge, der rabatterer den fremtidige pengestrøm for at nå frem til den aktuelle værdi. Diskonteringsrenten, der anvendes til nutidsværdien, bestemmes på baggrund af det aktuelle markedsafkast. Formlen for nutidsværdi kan udledes ved at diskontere den fremtidige pengestrøm ved hjælp af en forud specificeret rente (diskonteringsrente) og et antal år.

Formel For PV er angivet nedenfor:

PV = CF / (1 + r) t

Hvor,

• PV = nutidsværdi
• CF = Fremtidig pengestrøm
• r = Diskonteringsrente
• t = Antal år

I tilfælde af multiple forbindelser pr. År (betegnet med n), kan formlen for PV udvides som,

PV = CF / (1 + r/n) t*n

Eksempler på nuværende værdiformel (med Excel-skabelon)

Lad os tage et eksempel for at forstå beregningen af ​​nutidsværdien på en bedre måde.

Du kan downloade denne Excel-skabelon med nuværende værdi her - Nuværende værdiformel Excel-skabelon

Nuværende værdiformel - eksempel # 1

Lad os tage et simpelt eksempel på $ 2.000 fremtidig pengestrøm, der skal modtages efter 3 år. I henhold til den aktuelle markedsudvikling er den gældende diskonteringsrente 4%. Beregn værdien af ​​den fremtidige pengestrøm i dag.

Løsning:

Nuværende værdi beregnes ved hjælp af nedenstående formel

PV = CF / (1 + r) ^t

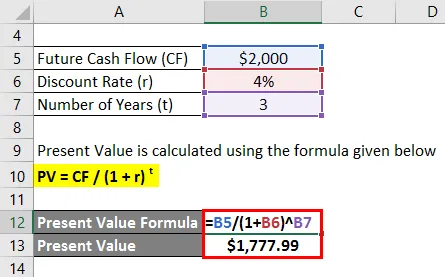
• Nuværende værdi = $ 2.000 / (1 + 4%) ³
• Nuværende værdi = $ 1.777.99

Derfor er den $ 2.000 kontantstrøm, der skal modtages efter 3 år, værd $ 1.777.99 i dag.

Nuværende værdiformel - eksempel # 2

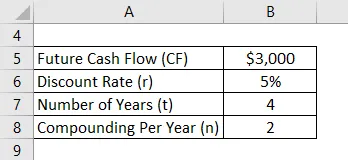
Lad os tage eksemplet med David, der søger et bestemt beløb i dag, således at han efter 4 år kan trække $ 3.000. Den gældende diskonteringssats er 5%, der sammensættes halvårligt. Beregn det beløb, som David skal indbetale i dag.

Løsning:

Nuværende værdi beregnes ved hjælp af nedenstående formel

PV = CF / (1 + r / n) ^{t * n}

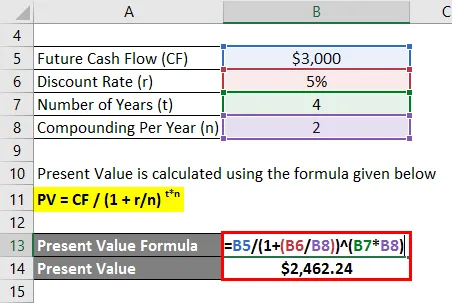
• Nuværende værdi = $ 3.000 / (1 + 5% / 2) ^{4 * 2}
• Nuværende værdi = $ 2.462.24

Derfor er David forpligtet til at indbetale $ 2.462 i dag, så han kan trække $ 3.000 efter 4 år.

Nuværende værdiformel - eksempel # 3

Lad os tage et andet eksempel på John, der vandt et lotteri, og i henhold til dets betingelser er han berettiget til årlig kontantudbetaling på $ 1.000 for de næste 4 år. Diskonteringsrenten er 4%. Beregn nutidsværdien af ​​alle fremtidige pengestrømme fra slutningen af ​​det indeværende år.

Løsning:

Nuværende værdi beregnes ved hjælp af nedenstående formel

PV = CF / (1 + r) ^t

For det første år,

• Nuværende værdi = $ 1.000 / (1 + 4%) ¹
• Nuværende værdi = $ 961, 54

For andet år,

• Nuværende værdi = $ 1.000 / (1 + 4%) ²
• Nuværende værdi = $ 924.56

I ^tredje år,

• Nuværende værdi = $ 1.000 / (1 + 4%) ³
• Nuværende værdi = $ 889, 00

For 4. år

• Nuværende værdi = $ 1.000 / (1 + 4%) ⁴
• Nuværende værdi = $ 854, 80

Nuværende værdi for hele året beregnes som:

• Nuværende værdi = $ 961, 54 + $ 924, 56 + $ 889, 00 + $ 854, 80
• Nuværende værdi = $ 3.629, 90

Derfor er nutidsværdien af ​​Johns lotterivinster $ 3.629, 90 .

Forklaring

Formlen for nutidig værdi kan afledes ved hjælp af følgende trin:

Trin 1: Find for det første den fremtidige pengestrøm, der er betegnet med CF.

Trin 2: Vælg derefter diskonteringsrenten baseret på det aktuelle markedsafkast. Det er den kurs, hvorpå de fremtidige pengestrømme skal diskonteres, og det betegnes med r.

Trin 3: Find derefter antallet af år, indtil den fremtidige pengestrøm begynder, og det betegnes med t.

Trin 4: Endelig kan formlen for nutidig værdi udledes ved at diskontere den fremtidige likviditetsstrøm (trin 1) ved hjælp af diskonteringsrente (trin 2) og et antal år (trin 3) som vist nedenfor.

PV = CF / (1 + r) ^t

Trin 5: Hvis antallet af sammensætning pr. År (n) er kendt, kan formlen for nutidig værdi udtrykkes som,

PV = CF / (1 + r / n) ^{t * n}

Relevans og anvendelser af nutidsværdiformlen

Begrebet nutidsværdi er primært baseret på tidsværdien af ​​penge, der siger, at en dollar i dag er mere værd end en dollar i fremtiden. Der er imidlertid en begrænsning af beregningen af ​​nutidsværdien, da den antager, at den samme afkastrate ville blive optjent over hele perioden - ingen afkastprocent kan garanteres for investeringer, da forskellige markedsfaktorer kan påvirke afkastet negativt hvilket resulterer i erosion af nutidsværdien. Som sådan er antagelsen om en passende diskonteringsrente desto vigtigere for korrekt værdiansættelse af de fremtidige pengestrømme.

Lommeregner for nuværende værdi

Du kan bruge følgende beregning af nutidsværdien

CF
r
t
PV

PV =	CF = (1 + r) t
	0 = 0 (1 + 0) 0

Anbefalede artikler

Dette har været en guide til nutidsværdiformlen. Her diskuterer vi Sådan beregnes nutidig værdi sammen med praktiske eksempler. Vi leverer også en nutidsværdiberegner med downloadbar excel-skabelon. Du kan også se på de følgende artikler for at lære mere -

1. Vejledning til nuværdiefaktorformler
2. Eksempler på formel for varianalyse
3. Sådan beregnes prøvestandardafvigelse?
4. Befolkningsvariantformel med Excel-skabelon