Vektorer i Matlab - Typer af vektordrift med eksempler

Introduktion til vektorer i Matlab

En vektor er et lukket sæt elementer. I Matlab kan vi oprette vektorer ved hjælp af firkantede parenteser. Vektorer er en af illustrationer af arrays (en-dimensionel matrix). det kan repræsenteres på to måder rækkevektor og søjlevektor.

Række vektor

Det er et vandret sæt af elementer. Det er repræsenteret i firkantede parenteser. Hvert element adskilles af komma eller mellemrum.

X = (4 7 8) eller X = (4, 7, 8)

Søjlevektor

Det er et lodret sæt af elementer. Det er også repræsenteret i firkantede parenteser. Der er to måder at oprette kolonnevektorer først ved at adskille hvert element med en semikolon og en anden måde er at skrive hvert element på den næste række i kommandovinduet.

X = (4; 6; 7) eller

X = (4

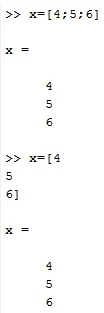
Vector operationer

Vektoroperatører er stort set klassificeret i to kategorier.

1. Aritmetisk operation

Lad os overveje to vektorer x og y med værdier x = (1 4 5 3) og y = (5 3 2 1) vi kan udføre forskellige operationer på disse to vektorer x og y.

en. Multiplikation: Denne funktion bruges til at multiplicere med enhver aritmetisk værdi til hele vektoren.

For eksempel:

mul = 3 * x

mul = 3 * (1 4 5 3)

mul = (3 12 15 9)

Syntaks: variable name = arithmetic constant * vector name

b. Trigonometrisk funktion: Vi kan anvende enhver trigonometrisk funktion på vektorlignende synd, cos, tan, cosec, sec osv.

Eksempel tri = cos (x)

Svaret er: 0.54 - 0.65 0.28 -0.99

Syntaks: variable name = trigonometric function name ( vector name )

Sum: Dette viser i alt (tilføjelse af) hele elementer i en vektor.

Eksempel

x = (1 4 5 3)

I alt = sum (x)

Output er i alt = 13

Syntaks: variable name = = sum ( vector name )

c. Længde: Den viser længden af en bestemt vektor, lad os en vektor p = (9 7 5 3 1 9 7 5 3 1)

Eksempel

p = (9 7 5 3 1 9 7 5 3 1)

Len = længde (p)

Output er Len = 10

d. Tilføjelse af vektorer: Tilføjelse af to eller flere vektorer er enkel betjening i Matlab, lad os overveje to vektorer p og q.

P = (4 6 3 2) og q = (5 7 9 1)

Tilføj = p + q

Output er Tilføj = (9 13 12 3)

Syntaks: vector name operator ( + ) vector name

Tilsvarende kan vi udføre subtraktion som sub = p - q

e. Multiplikation af vektorer: Hvis vi vil udføre multiplikation af to vektorer, fungerer en simpel multiplikationsoperatør (*) ikke. Derfor er vi nødt til at tilføje en dot operator ('.') Med en multiplikationsoperatør.

Eksempel:

P = (4 6 3 2) og q = (5 7 9 1)

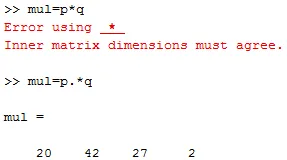
mul = p. * q

output er mul = (20 42 27 2)

Syntaks: variable name = vector name dot operator multiplication operator vector name

Antag, at jeg vil finde ud af en firkant af en bestemt vektor, eller at jeg kun vil multiplicere vektor med den vektor.

Derefter vil syntaks være squr = x. 2

2. Relationel drift

en. Lige med operatøren : denne operatør sammenligner hvert n hvert element fra to vektorer og giver output er nul og en form.

Eksempel

m = (2 5 8)

Og n = (5 5 3)

Som vi ved, er der tre elementer i vektor m og vektor n,

m == n

Ovenstående udsagn giver output som 0 1 0, hvilket betyder, at det første nej ikke er det samme, det andet tal er det samme, og det tredje nej ikke er det samme. O repræsenterer falsk og 1 repræsenterer sandt.

b. Mindre end operatør (<): Mindre end operatøren repræsenterer med symbolet '<'. vi kan sammenligne en given matrix med enhver aritmetisk konstant eller med en hvilken som helst anden vektor.

Eksempel

m = (3 2 4)

n = (1 1 1)

m <n

output vil være 0 0 0, det betyder, at alle tal er større end vektor n.

og hvis m <10

så vil output være 1 1 1, det betyder, at alle tal er mindre end 10.

c. Større end operatør (>): Større end operatøren repræsenterer ved symbolet ('>'). Vi kan sammenligne en given matrix med enhver aritmetisk konstant eller med enhver anden vektor.

Eksempel:

M = (3 2 4)

N = (1 1 1)

m> n

Output vil være 1 1 1, det betyder, at alle værdier er større end værdier af vektor n.

Konklusion - Vektorer i Matlab

I Matlab kan vi oprette forskellige typer vektorer, hvor vi kan udføre forskellige operationer som tilføjelse, subtraktion, multiplikation, kvadrat, firkantet rod, magt, skalering, vektormultiplikation, prikprodukt osv.

Anbefalede artikler

Dette er en guide til vektorer i Matlab. Her diskuterer vi de typer af vektordrift, der inkluderer aritmetisk og relationel drift sammen med nogle eksempler. Du kan også se på de følgende artikler for at lære mere -