
Introduktion til Fibonacci-serien i Python
Fibonacci-serien i Python, dette kaldes en række numre, hvor det næste tal er summen af de nuværende to numre.
For eksempel:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. så videre
Så her 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 og så videre.
Ser man på ovenstående, ville man have fået en viss idé om, hvad vi taler om.
I form af matematisk regel kan det imidlertid skrives som:

Hvor det niende nummer er summen af antallet på steder (n-1) og (n-2). Når det kommer til implementering af Fibonacci-serien, kan der være et antal kodesprog, gennem hvilke det kunne gøres.
Python er dog et meget brugt sprog i dag. Lad os se implementeringen af Fibonacci-serien gennem Python. Man skal være opmærksom på grundlæggende konditioneringsangivelser som løkken, hvis-ellers, mens løkke osv. I Python, før man fortsætter her. Hvis ikke, ville det være dejligt, hvis man kan revidere det og derefter tage det kommende indhold op. Her til demo formål bruger jeg spyder, som er IDE til python programmeringssprog. Man kan også bruge enhver anden IDE- eller Ipython-notebooks til udførelse af Python-programmerne.
Fibonacci-serien i Python
Lad os se implementeringen af Fibonacci-nummer og -serie, der overvejer første to elementer af Fibonacci er 0 og 1:
Du kan dog finpudse funktionen af Fibonacci som pr. Dit krav, men se det grundlæggende først og gradvist gå videre til andre.
Python-kode til at finde Nth Fibonacci-nummer
Kode 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Kode 2:
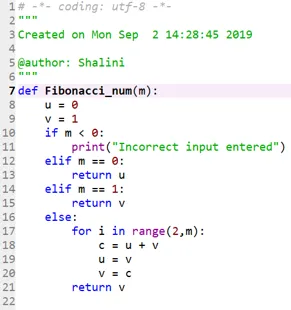
Produktion:
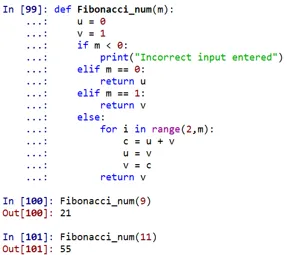
Som man kan se, ville Fibonacci-tallet på 9. pladsen være 21, og på 11. pladsen ville være 55.
- Her er "retracement_nummer" en defineret funktion, der tager sig af at finde Fibonacci-nummeret ved hjælp af visse betingelser. Denne funktion kan kaldes ved at specificere en hvilken som helst position.
Lad os nu se, hvordan man kan udskrive serier, indtil den nævnte position:
Kode:
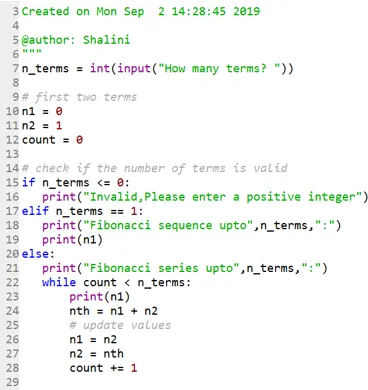
Produktion:
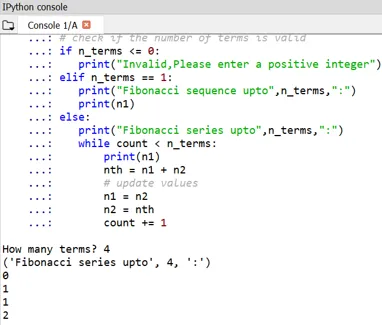
Man kan bemærke, at starten af Fibonacci-numre er defineret som 0 og 1.
- Hvis nogen ønsker at definere deres egne udtryk, kan det også gøres på samme måde ved at finpusse n1 og n2. Her er eksemplet til det:
Lad os sige, at vi nu ønsker, at vores udgangsbetingelser skal være: n1 = 3, n2 = 5
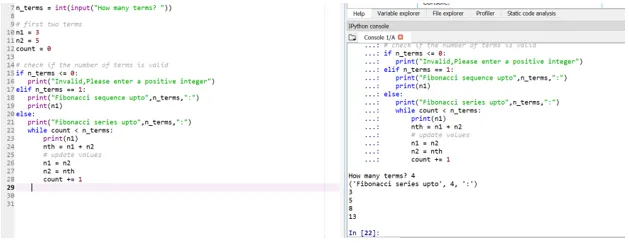
Så her vælges din 4. sæsonposition (brugerindtastning), baseret på dine udgangsbetingelser.
Metoder, gennem hvilke Fibonacci-serien kan genereres
Nedenfor er de tre metoder, gennem hvilke Fibonacci-serien kan genereres:
1. Gennem generatorer
Kode:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Produktion:
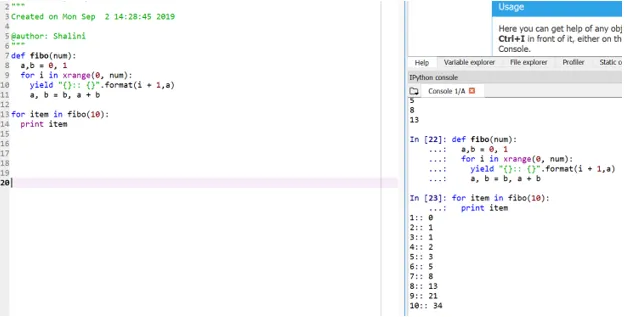
Denne metode kaldes “generator”, fordi funktionen xrange er en generator med numrene mellem 0 og num, og udbyttet er generatoren for formateret output.
Her er hvad xrange gør for dig:

Her er Fibonacci-serien blevet defineret i form af funktion, hvori inden for loop-, xrange- og udbyttefunktion tager sig af output.
2. Gennem for loop
Kode:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Produktion:

Som man kan se, er der brugt simple for loop til at udskrive Fibonacci-serien mellem 0 til 10. Inde i loop er der tildelt nye værdier til variablerne. U og v er standardværdierne for Fibonacci, der er indstillet til henholdsvis 0 og 1.
Når det gælder løkken, når den kører, er den nye u-værdi den gamle v-værdi, mens den nye v-værdi er summen af de gamle værdier for u og v. Dette fortsætter indtil slutningen af intervalværdierne.
3. Gennem rekursion
Kode:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Produktion:
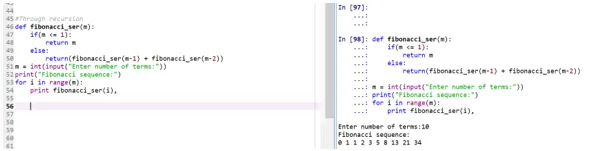
- Funktionen "retracement_ser" kalder sig selv til at udskrive Fibonacci-serien.
- Og dermed har metoden fået sit navn "rekursion".
Trin Følges her:
- Her er brugeren blevet bedt om at indtaste det sted, indtil hvilken Fibonacci-serien skal udskrives.
- Nummer passerer gennem funktionen "retracement_ser".
- Tilstanden bliver kontrolleret, hvis den angivne længde er mindre end 1 eller ikke. Hvis ja, gives resultatet med det samme.
- Men hvis længden er større end 1, foretages rekursive opkald til "retracement_ser" med argumenter, der har længde mindre end 1 og 2, dvs. retracement_ser (m-1) og retracement_ser (m-2).
- Rekursion giver derfor den ønskede output og udskriver den.
- Så kort sagt diskuterede vi tre måder til visning af Fibonacci-serien.
- Gennem for loop, gennem generatorer og gennem rekursion.
Alle tre Python-koder er opsummeret
Nedenfor er de tre python-koder:
1. Gennem generatorer
Kode:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Gennem for loop
Kode:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Gennem rekursion
Kode:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Sammenfattet ovenfor er alle procedurer, man skal øve sig for at få et godt greb om alle.
Produktion:
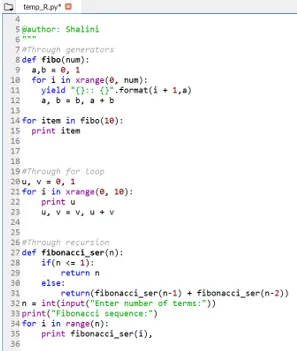
Konklusion
Gennemgå ovennævnte indhold af Fibonacci, ville man have krystalklar forståelse af Fibonacci-numre og -serier, der er specialiseret med python. En gang bliver man fortrolig med Fibonacci-seriens logik, at generere et andet sæt serier, arbejde med andre numre og med forskellige metoder vil nu være en cakewalk for dig. En logisk tilgang er den eneste måde at udmærke sig i dette.
Anbefalede artikler
Dette er en guide til Fibonacci-serien i Python. Her diskuterer vi Fibonacci-numre og -serier, specialiseret med python, genererer et andet sæt serier, arbejder med andre numre og med forskellige metoder. Du kan også gennemgå vores andre relaterede artikler for at lære mere -
- Tilfældig nummergenerator i Python
- Matematiske funktioner i Python
- Factorial i Python
- Indkapsling i Python
- Fibonacci-serien i Java
- Python-funktioner
- Factorial-program i JavaScript
- Tilfældig nummergenerator i Matlab
- Tilfældig nummergenerator i C #
- Indkapsling i JavaScript