Komplekse numre i MATLAB - Sådan genereres komplekst antal?

Introduktion til komplekse numre i MATLAB

Komplekse numre er kombinationen af reelle tal og imaginære tal i form af p + qi, hvor p og q er de reelle tal, og i er det imaginære tal. Et imaginært tal er defineret, hvor i er resultatet af en ligning a 2 = -1. Vi kan bruge i eller j til at betegne de imaginære enheder. Da komplekse tal bruges i enhver matematisk beregning, og Matlab bruges hovedsageligt til at udføre matematiske beregninger. Så komplekse tal udgør en vigtig del af at lære Matlab.

Generering af komplekse numre i MATLAB

Komplekse numre kan oprettes eller deklareres i Matlab ved hjælp af en 'kompleks' funktion. Vi kan også oprette komplekse tal ved at finde kvadratroten til ethvert negativt tal. I Matlab kan vi bruge i eller j til at betegne den imaginære del af det komplekse nummer.

eksempler

X = 4 + 5i

Her er X et komplekst tal, der indeholder 2 dele, dvs. reel og imaginær del. 4 er den virkelige del og 5 er den imaginære del. Vi kan finde de virkelige og imaginære dele ved hjælp af funktioner i Matlab.

a = reel (X) = 4 (Dette giver den reelle del af det komplekse antal)
b = imag (X) = 5 (Dette giver den imaginære del af det komplekse tal)
kompleks (6, 7) = 6 + 7i (Denne funktion bruges til at oprette komplekst tal)

Vi kan også oprette komplekse arrays i Matlab, som også kan erklæres ved hjælp af de komplekse funktioner.

a = kompleks (x, y)

Der er visse betingelser for x og y, som vi skal følge, ligesom x og y ikke skal være enkelt eller dobbelt. En kompleks skalar kan oprettes, hvis to input er skalar i naturen,

X = kompleks (5, 3)
X = 5.0000 + 3.0000i

Tilsvarende kan der oprettes en kompleks vektor, hvis vi har to input som vektorer.

X = uint8 ((4; 5; 6; 7));
Y = uint8 ((3; 5; 1; 2));
a = kompleks (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Vi kan oprette et komplekst tal, der kun har en skalar,

X = kompleks (10)
X = 10, 0000 + 0, 0000i

Der er visse betingelser, som input- og output-argumenterne skal følge,

Indgangsargumenterne indeholder virkelige og imaginære dele som x ethvert y. x og y skal være skalar, vektor, multidimensionel matrix eller matrix i MATLAB. x- og y-størrelsen skal være den samme. De skal være af den samme datatype, men der er få undtagelser, ligesom dobbelt kan bruges med enkelt og heltal kan kombineres med en dobbelt, der er skalær.

Arrayets output kan være vektor-, skalar-, matrix- eller multidimensionel array afhængigt af input-argumenterne. Størrelsen på output skal være den samme som input. Hvis input-argumenterne er af forskellige datatyper end output er bestemt af,

Hvis en af input-argumenterne er af en art, skal output også være enkelt.
Hvis en af input-argumenterne har et heltal, skal output være af en heltal datatype.

Vi kan kontrollere, om matrixen er reel eller imaginær ved hjælp af isreal funktion.

Kode:

X = (2+i, 1); Isreal(X)

Produktion:

Kode:

Isreal (X (2))

Produktion:

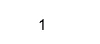
For at udtrække de virkelige og imaginære dele kan vi bruge reelle og imagefunktioner i Matlab som,

Kode:

real(X)

Produktion:

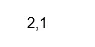
Kode:

imag(X)

Produktion:

Betjening og funktioner af komplekse numre i MATLAB

Der er flere operationer og funktioner, der kan udføres ved hjælp af komplekse tal i Matlab som

abs: Denne funktion bruges til at finde modulet til et hvilket som helst komplekst tal i form af p + qi. abs (2 + 3i) = firkantet rod af (2 2 + 3 2) = (13) 0, 5
vinkel: At finde fasevinklen på det komplekse tal.

Der er visse tip, der skal følges for, at komplekse tal i Matlab kan fungere korrekt,

Vi bør undgå at bruge i og j som en del af alle variabelnavne, da de bruges til at betegne de imaginære dele af det komplekse nummer.
Vi bør undgå at bruge j eller i, hvis den imaginære del er 1. I stedet for kan vi bruge 1j eller 1i.
Vi kan oprette en kompleks funktion i Matlab, når i og j bruges som variabelnavne i en del, input-argumenter er ikke af en enkelt eller dobbelt type, og den imaginære del er nul.

Konklusion

Komplekse numre bruges i det matematiske eller tekniske felt. Mange virkelige eller praktiske anvendelser kan beskrives ved hjælp af den imaginære del af komplekse tal. Så forståelse af brugen og anvendelsen af komplekse tal i forskellige platforme er vigtig, især hvis du har at gøre med et fysisk eller matematisk domæne.

Anbefalede artikler

Dette er en guide til komplekse numre i MATLAB. Her diskuterer vi introduktion og kompleks talgenerering i matlab inklusive dens eksempler med drift og funktion. Du kan også se på de følgende artikler for at lære mere-