F-testformel - Sådan beregnes F-test (eksempler med Excel-skabelon)

Indholdsfortegnelse:

Anonim

F-testformel (indholdsfortegnelse)

  • Formel
  • eksempler

Hvad er F-testformel?

F-test er en statistisk test, der hjælper os med at finde ud af, om to populationssæt, der har en normal fordeling af deres datapunkter, har den samme standardafvigelse eller -afvigelse. Men den første og vigtigste ting at udføre F-test er, at datasættene skal have en normal distribution. Dette anvendes til F-distribution under nulhypotesen. F-test er en meget vigtig del af analysen af ​​variation (ANOVA) og beregnes ved at tage forhold mellem to varianter af to forskellige datasæt. Som vi ved, at afvigelser giver os informationen om spredningen af ​​datapunkterne. F-test bruges også i forskellige tests som regressionsanalyse, Chow-test osv.

Formel FOR F-test:

Der er ingen enkel formel til F-Test, men det er en række trin, som vi skal følge:

Trin 1: For at udføre en F-test skal vi først definere nullhypotesen og alternativ hypotesen. Disse er givet af:

  • H0 (Null hypotese): Variation af 1. datasæt = Variation af et andet datasæt
  • Ha: Variation af 1. datasæt <Variance af 2. datasæt (til en lavere en-halet test)
  • Ha: Variation af 1. datasæt> Variation af et andet datasæt (til en øvre en-halet test)
  • Ha: Variation af 1. datasæt ≠ Variant af et andet datasæt (til en to-halet test)

Trin 2: Det næste, vi skal gøre, er, at vi er nødt til at finde ud af betydningsniveauet og derefter bestemme graden af ​​frihed for både tælleren og nævneren. Dette hjælper os med at bestemme deres kritiske værdier. Frihedsgrad er prøve størrelse -1.

Trin 3: F-testformel:

F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set

Trin 4: Find den kritiske F-værdi fra F-tabellen ved at tage en grad af frihed og niveau af betydning.

Trin 5: Sammenlign disse to værdier, og hvis en kritisk værdi er mindre end F-værdien, kan du afvise nulhypotesen.

Eksempler på F-testformler (med Excel-skabelon)

Lad os tage et eksempel for at forstå beregningen af ​​F-Test på en bedre måde.

Du kan downloade denne F-TEST formel Excel-skabelon her - F-TEST formel Excel-skabelon

F-testformel - eksempel # 1

Lad os sige, at vi har to datasæt A & B, der indeholder forskellige datapunkter. Udfør F-test for at afgøre, om vi kan afvise nulhypotesen på et 1% -niveau af betydning.

Datasæt:

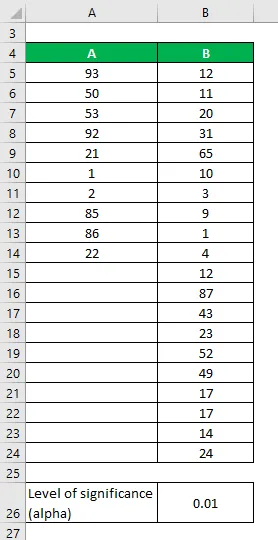
Løsning:

Nul hypotese: variation af A = variation af B

Frihedsgrad beregnes som

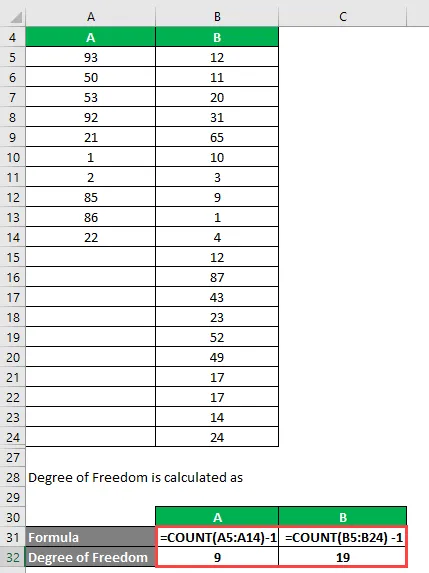
Grad af frihed

  • For A = 10 - 1 = 9
  • For B = 20 - 1 = 19

Variationen beregnes som:

  • Variation af A = 1385, 61
  • Variation af B = 521, 22

F-værdi beregnes ved hjælp af nedenstående formel

F-værdi = variation af 1. datasæt / variation af 2. datasæt

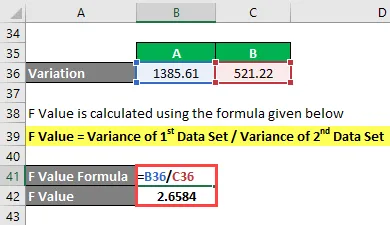
  • F-værdi = 1385, 61 / 521, 22
  • F-værdi = 2.6584

F-tabel:

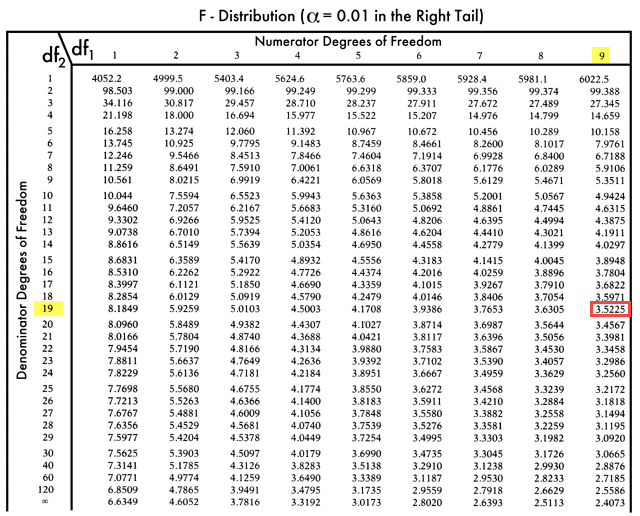
Så F kritisk værdi = 3.5225

Da F kritisk er større end F-værdien, kan vi ikke afvise nullhypotesen.

F-testformel - eksempel # 2

Antag, at du arbejder i en forskningsvirksomhed og ønsker at niveauet for kulstofoxidemission sker fra 2 forskellige cigaretmærker, og om de er markant forskellige eller ikke. I din analyse har du samlet følgende oplysninger:

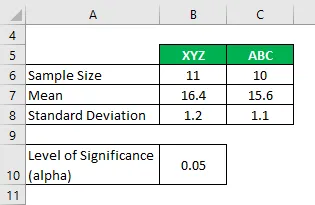
Løsning:

Frihedsgrad beregnes som

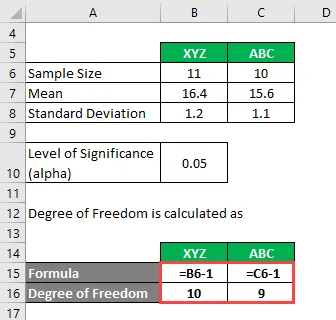
Grad af frihed

  • For XYZ = 11 - 1 = 10
  • For ABC = 10 - 1 = 9

Variationen beregnes som:

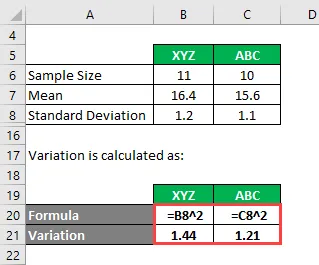
  • Variation af XYZ = 1, 2 2 = 1, 44
  • Variation af ABC = 1, 1 2 = 1, 21

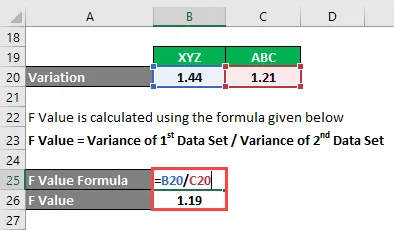
  • F-værdi = 1, 44 / 1, 21
  • F-værdi = 1, 19

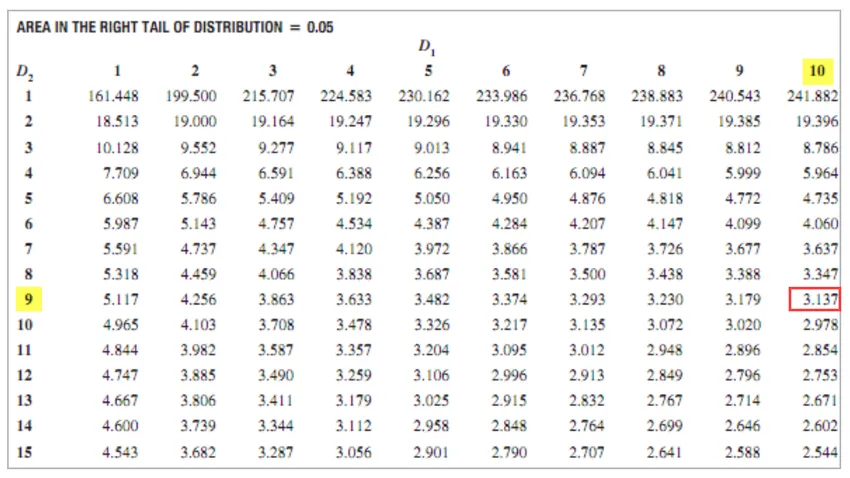
F Kritisk værdi = 3.137

Da F kritisk> F-værdi, kan nulhypotesen ikke afvises.

Forklaring

I eksemplerne ovenfor har vi set anvendelsen af ​​F-Test, og hvordan den udføres. Men der er et sæt antagelser, vi er nødt til at passe på, før vi udfører F-Test, ellers får vi ikke krævede resultater:

  • Den første ting er, at vi altid skal placere tælleren med højere variansværdi, mens vi beregner F-værdien. Så hvis F = V1 / V2, skal V1 være> V2
  • Hvis vi vil udføre 2 haletest, er vi nødt til at dele betydningsniveauet med 2, og det vil være det rigtige niveau for at finde den kritiske værdi
  • Vi bruger kun varians er F-værdiberegningen, og hvis vi får standardafvigelser, som i eksempel 2, skal de være kvadrat for at finde variansen.
  • Begge prøver skal være uafhængige af hinanden, og prøvestørrelse skal være mindre end 30
  • Befolkningssæt, hvor prøverne udtages, skal normalt fordeles

Dette er de vigtigste parametre / antagelse, der skal tages hånd om, mens du udfører F-Test.

Relevans og anvendelse af F-testformler

F-test, som diskuteret ovenfor, hjælper os med at kontrollere for ligheden mellem de to befolkningsvariationer. Så når vi har to uafhængige prøver, der er trukket fra en normal population, og vi ønsker at kontrollere, om de har samme variation eller ej, bruger vi F-test. F-test har også stor relevans i regressionsanalyse og også til test af betydningen af ​​R2. Så i et nøddeskal er F-Test et meget vigtigt værktøj i statistikker, hvis vi vil sammenligne variationen af ​​2 eller flere datasæt. Men man skal huske alle antagelserne, inden man udfører denne test.

Anbefalede artikler

Dette har været en guide til F-Test Formula. Her diskuterer vi, hvordan man beregner F-Test sammen med praktiske eksempler og downloadbar excel-skabelon. Du kan også se på de følgende artikler for at lære mere -

  1. T-fordelingsformel
  2. Formel til prissætning af obligationer
  3. Procentfejlformel
  4. Beregning af NOPAT-formlen