
Introduktion til matematikfunktioner i C
Denne artikel viser de forskellige matematiske funktioner, der bruges i C-programmeringssprog med illustration af arbejdskode. Computere foretager enorme matematiske beregninger og analyser af enormt antal, for at gøre det har vi brugt matematiske funktioner i C. Før vi starter med, skal vi vide, at C-sprog bruger overskrift / bibliotek kaldet Math.h til forskellige matematiske funktioner. Dette hjælper med at beregne trigonometriske operationer, logaritmer, absolutte værdier, firkantede rødder. Så lad os udforske de forskellige typer funktioner, der bruges i dette bibliotek. Alle disse funktioner tager dobbelt som datatype og returnerer de samme.
Forskellige matematiske funktioner i C.
Lad os se forskellige funktioner defineret i matematik. Matematikbiblioteket er kategoriseret i tre hovedtyper: Trigonometriske funktioner, matematikfunktioner, Log / expo-funktioner. For at implementere nedenstående funktioner er det obligatorisk at medtage eller i koden.
1. sal (dobbelt a)
Denne funktion returnerer den største heltalværdi ikke større end 'a' værdi. Det runder en værdi og returnerer en dobbelt som et resultat. Det opfører sig forskelligt for negative tal, da de runder til det næste negative tal.
Eks: etage (7.2) er 7, 0
etage (-7, 2) er -8, 0
Eksempel:
Dette program illustrerer, hvordan man beregner gulvet for den deklarerede værdi og runder til den næste værdi 10.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
Produktion:

2. loft ()
Syntaks:
double ceil (double b)
Denne funktion returnerer den mindste heltalværdi, der er større eller lig med b, og afrunder værdien opad. For en negativ værdi bevæger det sig mod venstre. Eksempel 3.4 returnerer -3 har output.
Eksempel:
Dette program forklarer ved at indtaste input i float-argumentet og returnerer loftsværdien.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
Produktion:

3. Sqrt ()
Denne funktion returnerer kvadratroten til et specificeret nummer.
Syntaks:
sqrt( arg)
Eksempel:
Nedenstående kode forklarer den mest kendte matematiske funktion sqrt () ved at tage 'n' værdier for at beregne kvadratroten for de forskellige 'n' værdier.
#include
#include
int main()
(
double n, output;
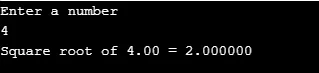
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
Produktion:
4. runde ()
Denne funktion afrunder den nærmeste værdi af en given input. Det kaster fejlen ud, hvis værdien er for stor. Andre funktioner som lround (), llround () runder også det nærmeste heltal.
Syntaks:
int round(arg)
Eksempel:
Nedenstående kode er meget enkel, hvilket afrundes til den nærmeste 'r' værdi i for loop.
#include
#include
int main ()
(
for(double r=110;r<=120;r+=1.1)
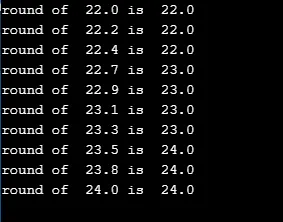
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
Produktion:
5.pow ()
Denne funktion vender tilbage til strømmen for det givne nummer (a b ). Det returnerer en hævet til styrken af b, som har to parametre base og eksponent.
Eksempel:
I kildekoden nedenfor giver vi en bruger mulighed for at indtaste en inputværdi for at beregne kraften i de givne to argumenter.
#include
#include
int main()
(
int r, ba, expr;
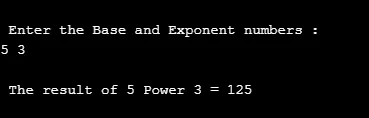
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
produktion:
6. trun ()
Denne funktion hjælper med at beskære den givne værdi. Det returnerer heltalværdier. Til trunkering af flydende og dobbeltværdier trunkef () bruges trunkl ().
Syntaks:
double trunc(a);
Eksempel:
Nedenfor kildekoden tager to inputværdier a, b for at afkorte de dobbelte værdier.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
Produktion:

7. fmod ()
Denne funktion returnerer resten for de givne to inputværdier, når m divideret med n.
Syntaks:
double fmod(double I, double j)
Eksempel:
I det nedenstående eksempel tager det to værdier fra brugeren at beregne resten ved hjælp af fmod () -funktionen.
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
Produktion:

Trigonometriske funktioner
Nedenfor er de forskellige funktioner i Trigonometric:
1. synd ()
Denne indbyggede funktion giver sinusværdi af det givne antal, beregner flydepunktværdier. asin () beregner bue, for hyperbolisk er det sinh ().
Syntaks:
return type sin(y);
y returnerer værdi i radianer og returtype tager dobbelt.
Eksempel:
I den følgende kildekode har jeg taget to forskellige inputværdier til at beregne sin-værdien og returnerer dobbelt.
#include
#include
int main()
(
double a;
double z;
a = 4.3;
z = sin(a);
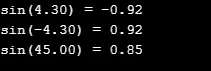
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
Produktion:
2. sinh ()
Denne matematikfunktion beregner trigonometrisk tangent-sinusværdi for det givne antal.
Syntaks:
double sinh(x);
Eksempel
I nedenstående kildekode beregnes synshyperbolic ved at angive en inputværdi.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
Produktion

3. cos ()
Denne matemafunktion bestemmer den trigonometriske kosinusværdi for det givne element.
Syntaks: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
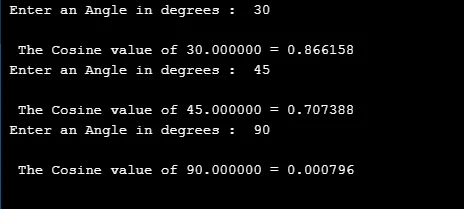
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
Produktion:
4. kosh ()
Det returnerer hyberbolisk kosinus for en given værdi.
Syntaks:
double cosh(y);
Eksempel
Nedenstående eksempel viser, at det tager to forskellige inputværdier at beregne hyperbol.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
Produktion

5. brunfarve ()
Denne matematiske biblioteksfunktion beregner tangensværdier for vinklen for det matematiske udtryk og måles i radianer.
Det kan erklæres som
double tan(arguments);
Eksempel
I den følgende kildekode beregnes solbrændingsværdien for de følgende vinkler, der øges ved hjælp af for loop.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
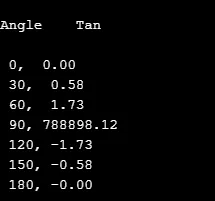
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
Produktion:
6. tanh ()
tanh () -funktion returnerer hyperbolsk tangens for den givne værdi. Det tager en enkelt parameter. Ud over at finde tangens til lang dobbelt- og flydende tanhl () og tanhf () bruges til beregning.
Syntaks:
double tanh( val);
Eksempel:
En tangent-hyberbolic beregnes for 'j' -værdier, der bruges til løkker. Lad os se, hvordan det fungerer.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
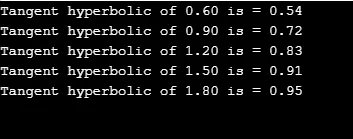
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
Produktion:
Log aritmetiske funktioner
Nedenfor er de forskellige funktioner i log aritmetik:
1. exp ()
Denne funktion udregner eksponentielt for en given værdi (e x ). Der er også andre undertyper som frexp (), Idexp (), der returnerer mantissa og ganget med kraften i x.
Syntaks:
return type exp(value);
Eksempel:
Programmet tager numerisk værdi fra brugeren for at beregne eksponenten for en given værdi og returnerer dobbelt.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
Produktion

2. log ()
Denne funktion returnerer logaritmeværdien for et givet nummer. (til basen e. log e )
Syntaks:
double log(arg);
Eksempel:
I det følgende eksempel beregnes logværdien for det givne nummer ved hjælp af funktion. Brugerdefineret funktion lgm () gør beregning, og funktion kaldes i hovedfunktionen.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
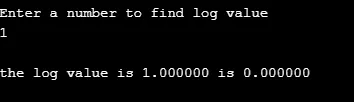
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
produktion:
Konklusion
Afslutningsvis har vi set forskellige matematiske funktioner, der bruges i C-programmering, og dette er de direkte biblioteksfunktioner, der skal bruges. C-programmer bruger disse funktioner til forskellige matematiske operationer. For at løse nogle komplekse versioner af beregninger er denne indbyggede funktion til fordel for matematisk orienteret programmeringssprog for at returnere enkle værdier.
Anbefalede artikler
Dette er en guide til matematiske funktioner i C. Her diskuterer vi forskellige matematiske funktioner i C med eksempler. Du kan også gennemgå vores andre foreslåede artikler -
- PHP Matematiske funktioner
- JavaScript-matematikfunktioner
- Overfør funktioner i Matlab
- JavaScript-strengfunktioner
- Introduktion til matematiske funktioner i Python
- Oversigt over matematiske funktioner i C #
- C Programmering af matrixmultiplikation
- Firkantet rod i PHP
- Eksempler på Square Root i JavaScript