
Introduktion til binomial distribution i R
Denne artikel beskriver, hvordan man bruger binomiale fordelinger i R til de få operationer, der er involveret i sandsynlighedsfordelinger. Forretningsanalyse bruger binomial sandsynlighed for et komplekst problem. R har adskillige indbyggede funktioner til beregning af binomialfordelinger, der bruges til statistisk interferens. Binomialfordelingen også kendt som Bernoulli-forsøg tager to typer succes p og fiasko S. Hovedmålet med binomialfordelingsmodellen er, at de beregner de mulige sandsynlighedsresultater ved at overvåge et specifikt antal positive muligheder ved at gentage processen et bestemt antal gange . De skal have to mulige resultater (succes / fiasko), derfor er resultatet dikotomt. Den foruddefinerede matematiske notation er p = succes, q = 1-p.
Der er fire funktioner forbundet med Binomial-distributioner. De er dbinom, pbinom, qbinom, rbinom. Den formaterede syntaks er angivet nedenfor:
Syntaks
- dbinom (x, størrelse, prob)
- pbinom (x, størrelse, prob)
- qbinom (x, størrelse, prob) eller qbinom (x, størrelse, prob, lavere_tail, log_p)
- rbinom (x, størrelse, prob)
Funktionen har tre argumenter: værdien x er en vektor af kvantiler (fra 0 til n), størrelse er antallet af sporforsøg, prob angiver sandsynlighed for hvert forsøg. Lad os se en efter en med et eksempel.
1) dbinom ()
Det er en densitets- eller distributionsfunktion. Vektorværdierne skal være et heltal skal ikke være et negativt tal. Denne funktion forsøger at finde et antal succes i et nr. af forsøg, der er faste.
En binomial fordeling tager størrelse og x-værdier. for eksempel størrelse = 6, de mulige x-værdier er 0, 1, 2, 3, 4, 5, 6 hvilket indebærer P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Produktion:
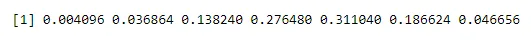
At gøre sandsynlighed for en
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Produktion:
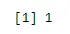
Eksempel 1 - Hospitalets database viser, at patienter, der lider af kræft, 65% dør af den. Hvad er sandsynligheden for, at 5 tilfældigt valgte patienter, hvoraf 3 vil komme sig?
Her anvender vi dbinom-funktionen. Sandsynligheden for, at 3 vil komme sig ved hjælp af densitetsfordeling på alle punkter.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Produktion:

For x-værdi 0 til 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Produktion:
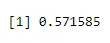
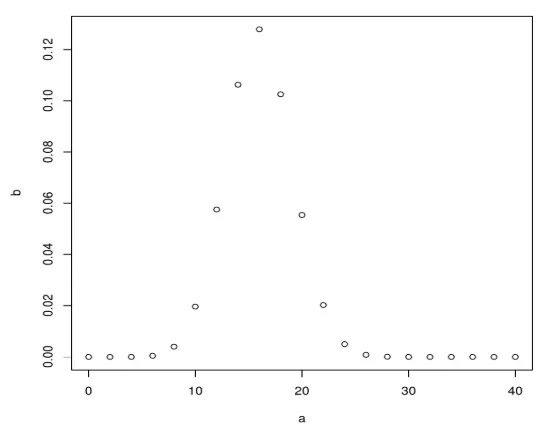
Derefter oprettes en prøve på 40 papirer og øges med 2 og opret også binomial ved hjælp af dbinom.
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
Det producerer følgende output efter udførelse af ovenstående kode. Binomialfordelingen er afbildet ved hjælp af plot () -funktion.
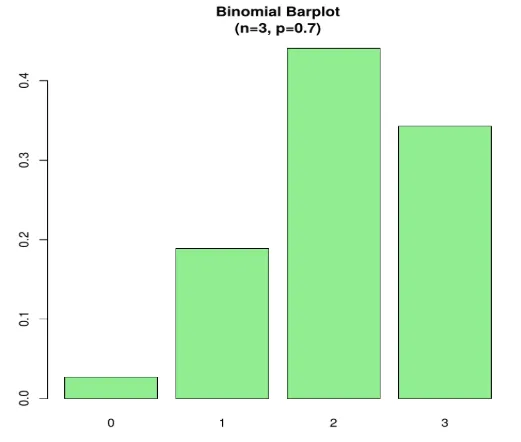
Eksempel 2 - Overvej et scenarie, lad os antage, at sandsynligheden for, at en studerende låner en bog fra et bibliotek er 0, 7. Der er 6 studerende på biblioteket, hvad er sandsynligheden for, at 3 af dem udlåner en bog?
her P (X = 3)
Kode:
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Nedenfor plott viser, når p> 0, 5, derfor er binomialfordeling positivt skæv som vist.
Produktion:
2) Pbinom ()
beregner kumulative sandsynligheder for binomial eller CDF (P (X <= x)).
Eksempel 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Produktion:

Eksempel 2: Dravid scorer en wicket på 20% af sine forsøg, når han boller. Hvis han boller 5 gange, hvad er sandsynligheden for, at han scorer 4 eller mindre wicket?
Sandsynligheden for succes er 0, 2 her, og i løbet af 5 forsøg, vi får
pbinom(4, size=5, prob=.2)
Produktion:
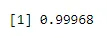
Eksempel 3: 4% af amerikanerne er sorte. Find sandsynligheden for 2 sorte studerende, når du tilfældigt vælger 6 studerende fra en klasse på 100 uden udskiftning.
Når R: x = 4 R: n = 6 R: p = 0. 0 4
pbinom(4, 6, 0.04)
Produktion:-
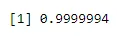
3) qbinom ()
Det er en kvantefunktion og gør det inverse af den kumulative sandsynlighedsfunktion. Den kumulative værdi stemmer overens med en sandsynlighedsværdi.
Eksempel: Hvor mange haler har en sandsynlighed på 0, 2, når en mønt kastes 61 gange.
a <- qbinom(0.2, 61, 1/2)
print(a)
Produktion:-
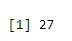
4) rbinom ()
Det genererer tilfældige tal. Forskellige resultater producerer forskellige tilfældige output, der bruges i simuleringsprocessen.
Eksempel:-
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Produktion:-

Hver gang vi udfører giver det tilfældige resultater.
rbinom(200, 4, 0.4)
Produktion:-

Her gør vi dette ved at antage resultatet af 30 møntvend i et enkelt forsøg.
rbinom(30, 1, 0.5)
Produktion:-
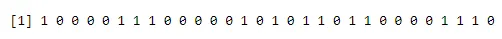
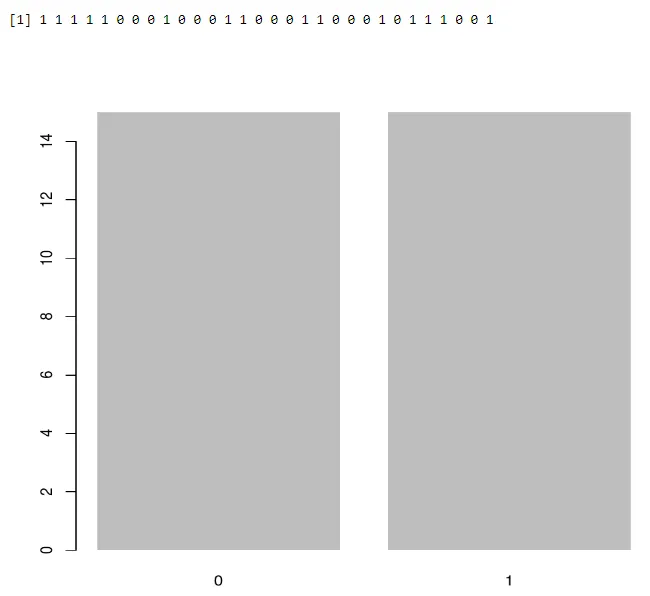
Brug af barplot:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Produktion:-
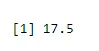
At finde gennemsnittet for succes
output <-rbinom(10, size=60, 0.3)
mean(output)
Produktion:-
Konklusion - Binomial distribution i R
Derfor har vi i dette dokument diskuteret binomial distribution i R. Vi har simuleret ved hjælp af forskellige eksempler i R studio og R uddrag og også beskrevet de indbyggede funktioner, der hjælper med at generere binomialberegninger. Binomial fordelingsberegning i R bruger statistiske beregninger. Derfor hjælper en binomial distribution med at finde sandsynlighed og tilfældig søgning ved hjælp af en binomialvariabel.
Anbefalede artikler
Dette er en guide til Binomial distribution i R. Her har vi drøftet en introduktion og dens funktioner forbundet med Binomial distribution sammen med syntaks og passende eksempler. Du kan også gennemgå vores andre foreslåede artikler for at lære mere -
- Binomial fordelingsformel
- Økonomi vs forretning
- Forretningsanalyseteknikker
- Linux-distributioner