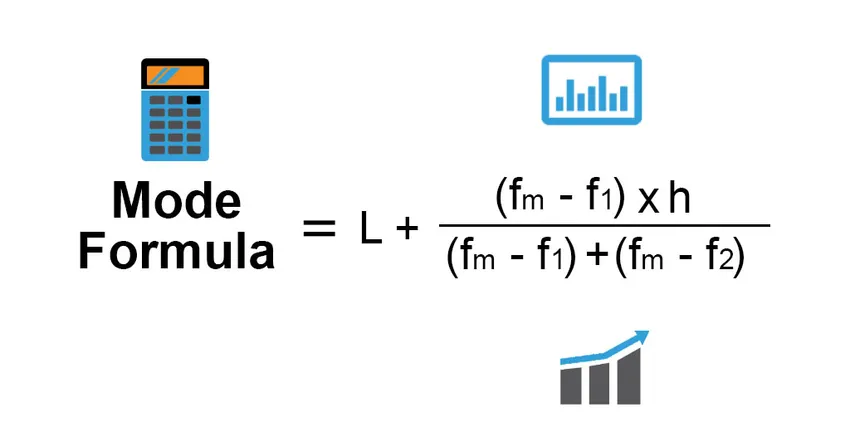
Tilstandsformel (indholdsfortegnelse)
- Formel
- eksempler
- Lommeregner
Hvad er tilstandsformlen?
De tre centrale mål for tendens er gennemsnit median og tilstand. Når alle tre bruges sammen til at udtrække meningsfuld analyse i datasættet. I dag i denne artikel vil vi drøfte tilstand, som også er en af nøglerne og den vigtige metode, der anvendes til den centrale tendens. Mode henviser til den hyppigst forekommende værdi i datasættet. Du kan finde en datatilstand med det normale datasæt, gruppedatasæt såvel som ikke-grupperede eller ikke-grupperede datasæt. Imidlertid forbliver det middel, der er mest almindeligt anvendt, stadig det bedste mål for central tendens på trods af eksistensen af middelværdi, median og tilstand. I denne artikel vil vi prøve at forstå tilstandsfunktionen, eksempler og forklaringer på hvert eksempel sammen med formlen og beregningerne.
Formlen til tilstand er: -
Mode = L + (fm−f1)h /(fm−f1)+(fm−f2)
Tilstandsformel for grupperede data:
Mode = L + (fm − f1) h / 2fm − f1 − f2
Hvor,
- L = Nedre grænse Mode for modalklasse
- fm = Frekvens af modalklasse
- f1 = Frekvens af klasse forud for modalklassen
- f2 = Frekvens af klasse, der følger den modale klasse
- h = Størrelse på klassens interval
Eksempler på tilstandsformel (med Excel-skabelon)
Lad os tage et eksempel for at forstå beregningen af tilstand på en bedre måde.
Du kan downloade denne Mode Formula Excel-skabelon her - Mode Formula Excel TemplateTilstandsformel - eksempel # 1
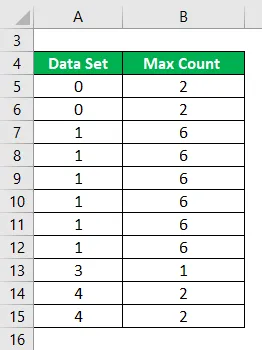
Hvor tilstand beregnes blot antallet af observationer i et datasæt, der forekommer det meste af tiden.
Beregn tilstanden for følgende datasæt.
Løsning:
En tilstand beregnes som:
Antal observationer i et datasæt, der forekommer det meste af tiden
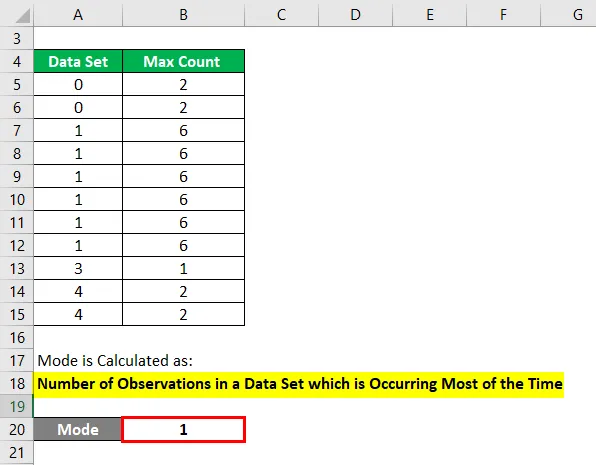
- Mode = 1
Tilstandsformel - eksempel # 2
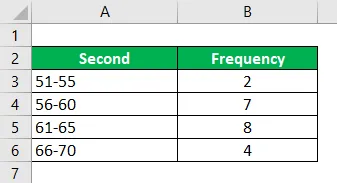
Beregn tilstanden ved hjælp af den givne information.
Løsning:
Bemærk: - Først skal den modale gruppe med den højeste frekvens identificere, hvis intervallet ikke er kontinuerligt, skal 0, 5 trækkes fra den nedre grænse-tilstand, og 0, 5 tilføjes fra den øvre grænse-tilstand. Derefter vil intervallet være
Modal gruppe beregnes som:
Modal gruppe, der er hyppigst, dvs. 60, 5-65, 5
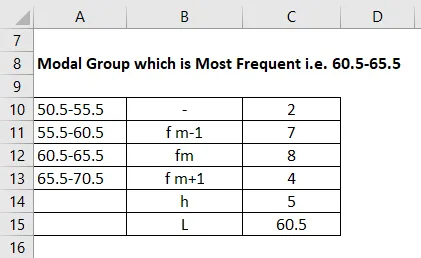
Så er den lavere frekvens af den modale gruppe, der er 4, i dette tilfælde tages som fm + 1, og fm-1 bliver 7 i dette eksempel. Og vi har fm, der er frekvensen som 8. Den (h) kaldes størrelsen på klassens interval er 5, som vi også overvejer startintervallet. L er 60, 5.
Funktionen beregnes ved hjælp af nedenstående formel
Mode = L + (fm − f1) h / (fm − f1) + (fm − f2)
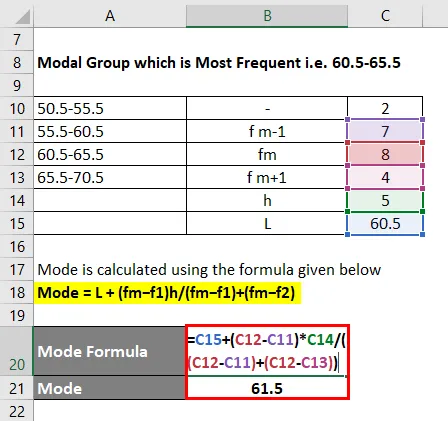
- Mode = 60, 5 + (8 - 7) * 5 / ((8 - 7) + (8 - 4))
- Mode = 61.5
Tilstandsformel - eksempel # 3
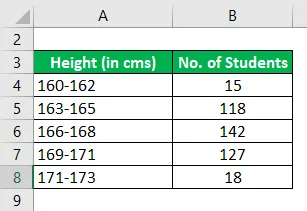
Følgende er fordelingen af højder i en bestemt klasse af studerende i en bestemt tilstand
Beregn tilstanden ved hjælp af den givne information.
Løsning:
Hvis intervallet ikke er kontinuerligt, skal 0, 5 trækkes fra tilstanden til nedre grænse, og 0, 5 tilføjes fra tilstanden øvre grænse. Derefter vil intervallet være
Modal gruppe beregnes som:
Modal gruppe, der er hyppigst, dvs. 165.5-168.5
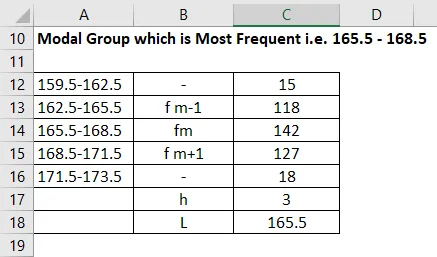
Funktionen beregnes ved hjælp af nedenstående formel
Mode = L + (fm − f1) h / (fm − f1) + (fm − f2)
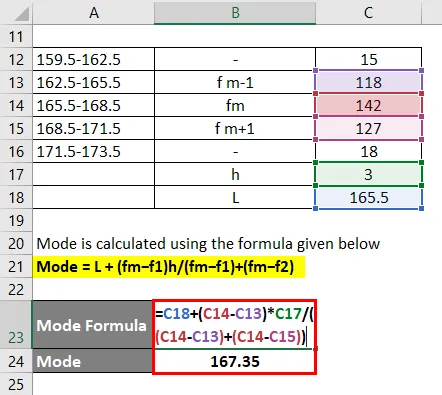
- Mode = 165, 5 + (142 - 118) * 3 / (142 - 118) + (142 - 127)
- Mode = 167, 35
Forklaring
Tilstanden kan enkelt forklares som den værdi, der hyppigst forekommer i datasættet. Og tilstanden ovenfor kan forklares, som når data er en gruppe, vi først skal beregne den modale funktion og også gøre dataene kontinuerlige for at beregne tilstanden til dataene. Modalklassen afgøres med den klasse, der har den højeste frekvens i datasættet.
Relevans og anvendelser af tilstand formel
- Gennemsnit, median og tilstand afslører forskellige aspekter af dine data. Enhver vil give dig en generel idé, men kan vildlede dig; at have alle tre giver dig et mere komplet billede
- For en normal fordeling har tilstanden, middelværdien, median den samme værdi, da tilstand er en normal fordeling. Analysetilstand isoleret afspejler ikke det rigtige billede, hvis du vil analysere det komplette datasæt, skal alle de tre statistiske mål analyseres detaljeret og fortolkes
- Tilstanden er let at forstå og enkel at beregne.
- Tilstanden påvirkes ikke af ekstremt store eller små værdier.
- Tilstanden kan placeres bare ved inspektion i ugrupperede data og diskret frekvensfordeling.
- Tilstanden kan være nyttig til kvalitative data.
- Tilstanden kan beregnes i en åben frekvenstabel.
- Tilstanden kan placeres grafisk
- Mode bruges mest af dataforskere
- Tilstand er, at det ikke vil give os et meget godt mål for central tendens, når det mest almindelige mærke er langt væk fra resten af dataene i datasættet
Mode Formula Calculator
Du kan bruge følgende Mode Formula Calculator
| L | |
| fm | |
| f1 | |
| f2 | |
| h | |
| Tilstandsformel | |
| Tilstandsformel = | L + (fm - f1) xh / (fm - f1) + (fm - f2) |
| = | 0 + (0 - 0) x 0 / (0 - 0) + (0 - 0) = 0 |
Anbefalede artikler
Dette er en guide til Mode Formula. Her diskuterer vi, hvordan man beregner Mode Formula sammen med praktiske eksempler. Vi leverer også en tilstandskalkulator med en downloadbar excel-skabelon. Du kan også se på de følgende artikler for at lære mere -
- Eksempler på Gordon Growth Model Formula
- Formel til beregning af model for kapitalforvaltning
- Lommeregner for formel for total udgiftsforhold
- Poisson-distributionsformel (eksempler med Excel-skabelon)