Vægtet gennemsnitformel (indholdsfortegnelse)
- Vægtet gennemsnitformel
- Vægtet gennemsnitskalkulator
- Vægtet gennemsnitformel i Excel (med Excel-skabelon)
Vægtet gennemsnitformel
Formlen til beregning af det vejede gennemsnit er som følger:
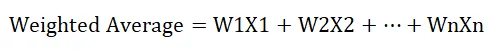
Hvor,
- W angiver relativ vægt (i%)
- X angiver værdi
Eksempler på vægtet gennemsnitformel
Lad os se nogle få eksempler til at forstå vægtet gennemsnitformel:
Eksempel 1
Lad os antage, at Anand har investeret pengene i følgende forholdsmæssige forhold: 40% i investering A, 20% i investering B og 40% i investering C. Disse investeringer har en afkastrate som følger: Investering A som 15%, investering B som 10 % og investering C som henholdsvis 20%. Vi er nødt til at beregne et vægtet gennemsnit for de afkastrater, Anand ville modtage.
Her,
- Vi har relative vægte for investeringerne A, B & C som henholdsvis 40%, 20% og 40%.
- Og værdi (afkast) for investeringerne A, B & C som henholdsvis 15%, 10% og 20%.
Ved at bruge den vægtede gennemsnitformel får vi-
- Vægtet gennemsnit = W1 X1 + W2 X2 + …… + Wn Xn
- Vægtet gennemsnit = 40% * 15% + 20% * 10% + 40% * 20%
- Vægtet gennemsnit = 16%
Dette viser, at Anand modtager 16% vægt gennemsnitligt afkast fra investeringerne A, B & C.
Eksempel 2
Lad os antage, at Anand har tilmeldt sig et matematik-kursus, hans endelige karakter vil blive bestemt ud fra følgende kategorier: prøver 30%, afsluttende eksamen 40%, quizzer 15% og hjemmearbejde 15%.
Anand har scoret følgende karakter i hver kategori: Tests-80, afsluttende eksamen-65, quizzer-85, hjemmearbejde-90. Nu skal vi finde ud af den samlede karakter af Anand.
For at beregne et vægtet gennemsnit med procenter, skal hver kategoriværdi først ganges med dens procentdel. Derefter skal alle disse nye værdier tilføjes sammen.
Her,
Vi har relative vægte for følgende kategorier som følger:
- Test 30%
- Afsluttende eksamen 40%
- quizzer 15%
- hjemmearbejde 15%
Og værdi (mærker) for kategorierne som
- Tests-80
- Afsluttende eksamen-65,
- quizzer-85
- lektier-90
Ved at bruge den vægtede gennemsnitformel får vi-
- Vægtet gennemsnit = W1 X1 + W2 X2 + …… + WnXn
- Vægtet gennemsnit = (30% * 80) + (40% * 65) + (15% * 85) + (15% * 90)
- Vægtet gennemsnit = 76, 25 eller 76%
Dette viser, at den samlede karakter af Anand er 76%.
Eksempel 3
Lad os antage, at Jagriti har investeret penge i aktier i forskellige virksomheder. Jagriti-porteføljen udgør 30% i Aktie A, 15% i Aktie B, 30% i Aktie C og de resterende 25% i Aktie D. Det forventede afkast i henhold til den aktuelle markedssituation på disse Aktier er som følger: Afkast på Aktie A er 15%, afkast på lager B er 12%, afkast på aktie C er 17% og afkast på aktie D er henholdsvis 16%. Jagriti ønsker at beregne sit gennemsnitlige afkast på porteføljen i henhold til den aktuelle markedssituation.
Her,
- Vi har relative vægt på lagrene i porteføljen som følger: A, B, C & D som henholdsvis 30%, 15%, 30% og 25%.
- Og værdi (Return Rate) for lagrene som følger: A, B, C & D som henholdsvis 15%, 12%, 17% og 16%.
Ved at bruge den vægtede gennemsnitformel får vi-
- Vægtet gennemsnit = W1 X1 + W2 X2 + W3 X3 + W4 X4 …… + Wn Xn
- Vægtet gennemsnit = (30% * 15%) + (15% * 12%) + (30% * 17%) + (25% * 16%)
- Vægtet gennemsnit = 0, 154 eller 15, 4%
Dette viser, at Jagriti modtager 15, 4% vægt gennemsnitligt afkast fra porteføljen af aktier A, B, C og D.
Forklaring af vægtet gennemsnitformel
Den vejede gennemsnitformel bruges til beregning af gennemsnitsværdien for et bestemt sæt tal med forskellige niveauer af relevans. Vægtene skal være repræsenteret i procent af total relevans. De tagede vægte skal være lig med 100% eller 1.
For at beregne vægtet gennemsnitformel har vi brug for relativ vægt og værdi.
Den første komponent er relativ vægtning, og den anden komponent er værdiindgange. For at beregne det vægtede gennemsnit skal vi have en specifik vægtning for hver variabel, der tages som værdi, og vægten skal svare til 100%.
Betydning og anvendelse af vægtet gennemsnitformel
Det vejede gennemsnit bruges i forskellige finansielle formler. Få eksempler på Vægtet gennemsnit beta og en vægtet gennemsnitlig kapitalomkostning (WACC).
Vi er bekendt med ideen om at finde det athematiske middelværdi eller gennemsnit for en række varer. Vi kan blot tilføje værdier for alle elementerne og dele det med det samlede antal poster til beregning af gennemsnittet. Dette fungerer kun, hvis alle emner vægtes lige. For at beregne de gennemsnitlige månedlige mobilregninger i et år kan vi for eksempel blot tilføje de samlede fakturerede beløb for de sidste tolv måneder og dele dem med tolv, så kan vi få en grov idé om den gennemsnitlige faktura, der er betalt, da mobilen faktureringscyklus er stort set for den samme periode, dvs. en måned.
Lad os nu sige, at du vil beregne den aktuelle gennemsnitlige kursuskarakter i din matematikklasse. Normalt tildeler de fleste af klasserne forskellige vægt til eksamener end til lektieopgaver, intern test og konkurrencer. I dette tilfælde skal du beregne et vægtet gennemsnit, der tager den specifikke vægt til hvert emne for at beregne din kursuskarakter.
Eksempel på nogle få tilfælde, hvor man skal bruge et vægtet gennemsnit i stedet for et simpelt gennemsnit. Første tilfælde - Når vi ønsker at beregne et gennemsnit, der har forskellige procentvise værdier for forskellige kategorier. Ovenstående eksempel på kurset er en af de lignende tilfælde. Og for det andet når vi har en stor gruppe af genstande med en anden regelmæssighed.
Hvis en virksomhed har en stor udsving i salget på grund af produktionen af et sæsonbestemt produkt, kan de bruge den vejede gennemsnitformel. Og virksomheden ønsker at beregne gennemsnittet for deres variable udgifter, så kan virksomheden bruge den vejede gennemsnitformel og tage salget som vægt for at få en bedre forståelse af deres udgifter. Og kan sammenligne det beløb, de producerer eller sælger.
Vægtet gennemsnitskalkulator
Du kan bruge følgende vægtet gennemsnitskalkulator
| W 1 | |
| X 1 | |
| W 2 | |
| X 2 | |
| W 3 | |
| X 3 | |
| W 4 | |
| X 4 | |
| Vægtet gennemsnitformel | |
| Vægtet gennemsnit Formel = | W 1 * X 1 + W 2 * X 2 + W 3 * X 3 + W 4 * X 4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Vægtet gennemsnitformel i Excel (med Excel-skabelon)
Her vil vi gøre det samme eksempel på den vægtede gennemsnitformel i Excel. Det er meget let og enkelt. Du skal angive de to indgange, dvs. relative vægte og afkasthastighed.
Du kan nemt beregne det vægtede gennemsnit ved hjælp af formler i den medfølgende skabelon.
vægt gennemsnitligt afkast fra investeringerne A, B & C beregnes som:

samlet karakter af Anand beregnes som:

vægt Alders gennemsnitligt afkast fra porteføljen af aktier A, B, C og D beregnes som:
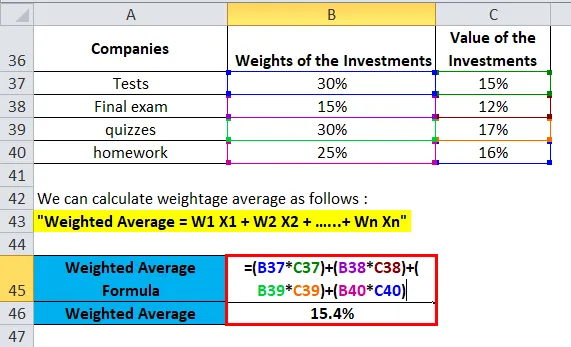
Du kan downloade denne Vægtet gennemsnit Formel Excel-skabelon her - Vægtet gennemsnit Formel Excel-skabelon
Anbefalede artikler
Dette har været en guide til en vægtet gennemsnitformel. Her diskuterer vi dens anvendelser sammen med praktiske eksempler. Vi giver dig også en vægtet gennemsnitskalkulator med downloadbar excel-skabelon. Du kan også se på de følgende artikler for at lære mere -
- Sådan beregnes omkostningsforhold?
- Beregn kapitalmultiplikator med eksempler
- Brug af bruttofortjenestemarginalformlen
- Vejledning til beregning af omsætning af tilgodehavender