Introduktion til hierarkisk klynge-algoritme
Den hierarkiske klynge-algoritme er en maskinoplæringsteknologi, der ikke overvåges. Det sigter mod at finde en naturlig gruppering baseret på dataens karakteristika.
Den hierarkiske klynge-algoritme sigter mod at finde indlejrede grupper af data ved at opbygge hierarkiet. Det svarer til den biologiske taksonomi for plante- eller dyreriget. Hierarkiske klynger er generelt repræsenteret ved hjælp af det hierarkiske træ kendt som et dendrogram.
Typer af hierarkisk klynge-algoritme
Hierarkiske grupperingsalgoritmer er af 2 typer:
- splittende
- agglomerative
1. Opdelende
Dette er en top-down tilgang, hvor den oprindeligt betragter alle data som en gruppe og derefter iterativt opdeler dataene i undergrupper. Hvis antallet af en hierarkisk klyngerealgoritme er kendt, stoppes opdelingsprocessen, når antallet af klynger er opnået. Ellers stopper processen, når dataene ikke kan opdeles mere, hvilket betyder, at undergruppen opnået fra den aktuelle iteration er den samme som den, der blev opnået fra den forrige iteration (man kan også overveje, at opdelingen stopper, når hvert datapunkt er en klynge ).
2. Agglomerativ
Det er en bottom-up tilgang, der er afhængig af sammenlægning af klynger. Oprindeligt er dataene opdelt i m singleton-klynger (hvor værdien af m er antallet af prøver / datapunkter). To klynger er slået sammen til en iterativt, hvilket reducerer antallet af klynger i hver iteration. Denne proces med fusionering af klynger stopper, når alle klynger er blevet fusioneret til en, eller antallet af ønskede klynger opnås.
På niveau 1 er der m-klynger, der reduceres til 1 klynge på niveau m. Disse datapunkter, der bliver slået sammen til dannelse af en klynge på et lavere niveau, forbliver også i den samme klynge på de højere niveauer. Antag f.eks., At der er 8 punkter x1..x8, så indledningsvis er der 8 klynger på niveau 1. Antag, at punkter x1 og x2 slås sammen i en klynge på niveau 2, derefter indtil niveau 8, de forbliver i den samme klynge.
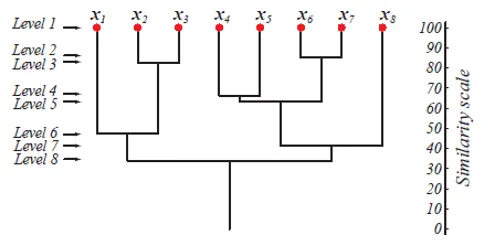
Ovenstående figur viser en dendrogram-repræsentation af agglomeration-klyngestrategien for 8 datapunkter såvel som lighedskalaen svarende til hvert niveau.
Klyngens niveauer giver os en idé om, hvor længe datapunkterne i klyngerne er. Som vist i fig. 1, bliver datapunkterne tidligere flettet ind i en klynge, ligner de. Så datapunkterne i en klynge på niveau 2 (f.eks. X2 og x3) er mere ens end datapunkterne i en klynge på niveau 6 (f.eks. X1 og x2).
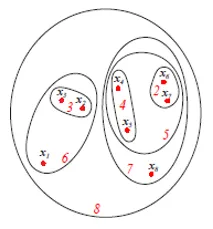
Ovenstående figur viser sæt- eller Venn-diagram-repræsentationen af den agglomerative klyngeforhold i de ovennævnte 8 datapunkter. Både dendrograms og sæt repræsentationer kan bruges til gruppering. Imidlertid er et dendrogram normalt foretrukket aktivrepræsentation kan ikke kvantitativt repræsentere klyngelighederne.
Trin til hierarkisk klynge-algoritme
Lad os følge de følgende trin for den hierarkiske klynge-algoritme, der er givet nedenfor:
1. Algoritme
Agglomerativ hierarkisk klynge-algoritme
- Begynd at initialisere c, c1 = n, Di = (xi), i = 1, …, n '
- Gør c1 = c1 - 1
- Find nærmeste klynger, sig, Di og Dj
- Flet Di og Dj
- Indtil c = c1
- Returner c-klynger
- Ende
Denne algoritme begynder med n klynger oprindeligt, hvor hvert datapunkt er en klynge. Med hver iteration reduceres antallet af klynger med 1, efterhånden som de 2 nærmeste klynger slås sammen. Denne proces fortsætter, indtil antallet af klynger reduceres til den foruddefinerede værdi c.
Hvordan beslutter jeg, hvilke klynger der er tæt på?
Det er defineret ved hjælp af adskillige afstandsmetriker, der er som følger:
- Den minimale afstand mellem klyngerne dmin (Di, Dj). Nyttigt til single.
- Den maksimale afstand mellem klyngerne dmax (Di, Dj). Nyttigt til komplet.
- Den gennemsnitlige afstand mellem klyngerne davg (Di, Dj).
Hvad er enkelt kobling og komplet link?
- Når dmin (di, dj) bruges til at finde afstanden mellem to klynger, og algoritmen slutter, hvis afstanden mellem de nærmeste klynger overstiger en tærskel, kaldes algoritmen en enkelt koblingsalgoritme.
- Når dmax (Di, Dj) bruges til at finde afstanden mellem to klynger, og algoritmen slutter, hvis afstanden mellem de nærmeste klynger overstiger en tærskel, kaldes algoritmen en komplet koblingsalgoritme.
- Lad os betragte hvert datapunkt som en knude på en graf. Der er en kant mellem to datapunkter, hvis de hører til den samme klynge. Når to nærmeste klynger slås sammen, tilføjes en kant. Det kaldes en enkelt forbindelse, fordi der findes en unik sti fra den ene knude til den anden.
- Den komplette koblingsalgoritme fusionerer to klynger ved at minimere afstanden mellem de to fjerneste punkter.
- En enkelt koblingsalgoritme genererer et spændende træ. Denne algoritme er dog modtagelig for støj. En komplet koblingsalgoritme genererer en komplet graf.
Hvad er tidskompleksiteten af algoritmen?
Antag, at vi har n mønstre i d-dimensionelt rum, og vi bruger dmin (Di, Dj) til at danne c-klynger. Vi er nødt til at beregne n (n - 1) inter-point-afstande - som hver er en O (d 2 ) -beregning - og placere resultaterne i en inter-point distancetabel. Rumkompleksiteten er O (n 2 ). At finde det minimale afstandspar (for den første sammenlægning) kræver, at vi går gennem den komplette liste og holder indekset for den mindste afstand.
For det første agglomerative trin er kompleksiteten således O (n (n - 1) (d2 + 1)) = O (n 2 d2). For et andet vilkårligt agglomerationstrin (dvs. fra c1 til c1 - 1) går vi blot gennem n (n - 1) - c1 "ubrugte" afstande på listen og finder de mindste, hvor x og x 'ligger i forskellige klynger . Dette er igen O (n (n − 1) −c1). Den samlede tidskompleksitet er således O (cn 2 d 2 ) og under typiske forhold n >> c.
2. Visualisering
Når dataene er opdelt i klynger, er det en god praksis at visualisere klyngerne for at få en idé om, hvordan ser grupperingerne ud. Men det er vanskeligt at visualisere disse højdimensionelle data. Derfor bruger vi Principal Component Analysis (PCA) til visualisering. Efter PCA opnår vi datapunkterne i det lave dimensionelle rum (generelt 2D eller 3D), som vi kan plotte for at se gruppering.
Bemærk: Høj dimension betyder et stort antal funktioner og ikke et antal datapunkter.3. Evaluering
En af metoderne til evaluering af klynger er, at afstanden mellem punkterne mellem klyngerne (inter-klynge-afstand) skal være meget mere end afstanden til punkterne inden i klyngen (intracluster afstand).
Konklusion
Følgende er de få vigtigste takeaways:
- Den hierarkiske klyngerealgoritme bruges til at finde indlejrede mønstre i data
- Hierarkisk klynge er af to typer - Opdelende og agglomerativ
- Dendrogram og sæt / Venn-diagram kan bruges til repræsentation
- Enkelt kobling fusionerer to klynger ved at minimere den minimale afstand mellem dem. Det danner en spænding
- Komplet kobling fusionerer to klynger ved at minimere den maksimale afstand mellem Det danner en komplet graf.
- Den samlede tidskompleksitet af hierarkisk klyngerealgoritme er O (cn 2 d 2 ), hvor c er det foruddefinerede antal klynger, n er antallet af mønstre og d er det d-dimensionelle rum i n mønstre.
Anbefalede artikler
Dette er en guide til den hierarkiske klynge-algoritme. Her diskuterer vi typer og trin i hierarkiske grupperingsalgoritmer. Du kan også se på de følgende artikler for at lære mere-
- Hierarkisk klynge-analyse
- Hierarkisk klynge i R '
- Clustering algoritme
- Hvad er klynge i datamining?
- Hierarkisk klynge | Agglomerativ og opdelende klynge
- C ++ algoritme | Eksempler på C ++ algoritme