
Margin of Error Formula (Indholdsfortegnelse)
- Margin of Error Formula
- Eksempler på margin af fejlformel (med Excel-skabelon)
- Margen for fejlformelberegner
Margin of Error Formula
I statistikken beregner vi konfidensintervallet for at se, hvor værdien af dataene for prøvestatistikken vil falde. Intervallet for værdier, der er under og over prøvestatistikken i et konfidensinterval er kendt som Margin of Error. Med andre ord er det dybest set graden af fejl i stikprøvestatistikken. Højere fejlmargin, jo mindre er tilliden til resultaterne, fordi graden af afvigelse i disse resultater er meget høj. Som navnet antyder, er fejlmargenen et interval af værdier over og under de faktiske resultater. For eksempel, hvis vi får et svar i en undersøgelse, hvor 70% mennesker har svaret "godt" og fejlmargenen er 5%, betyder det, at 65% til 75% af befolkningen generelt synes, at svaret er "godt" .
Formlen for Margin of Error -
Margin of Error = Z * S / √n
Hvor:
- Z - Z score
- S - Standardafvigelse for en befolkning
- n - Prøvestørrelse
En anden formel til beregning af fejlmargen er:
Margin of Error = Z * √((p * (1 – p)) / n)
Hvor:
- p - Prøveproportion (brøkdel af prøven, der er en succes)
For at finde den ønskede z-score skal du kende prøveens konfidensinterval, fordi Z-score er afhængig af det. Nedenstående tabel er vist for at se forholdet mellem et konfidensinterval og z-score:
| Konfidensinterval | Z - score |
| 80% | 1, 28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Når du kender konfidensintervallet, kan du bruge den tilsvarende z-værdi og beregne fejlmargenen derfra.
Eksempler på margin af fejlformel (med Excel-skabelon)
Lad os tage et eksempel for at forstå beregningen af Margin of Error på en bedre måde.
Du kan downloade denne Margin of Error Template her - Margin of Error TemplateMargin of Error Formula - Eksempel # 1
Lad os sige, at vi foretager en undersøgelse for at se, hvilken karakter score, som universitetsstuderende får. Vi har valgt 500 studerende tilfældigt og spurgt om deres karakter. Gennemsnittet heraf er 2, 4 ud af 4, og standardafvigelsen er 30%. Antag, at konfidensintervallet er 99%. Beregn fejlmargenen.
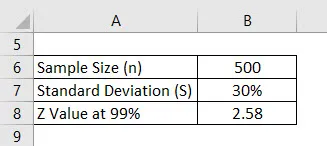
Løsning:
Fejlmargen beregnes ved hjælp af nedenstående formel
Fejlmargen = Z * S / √n
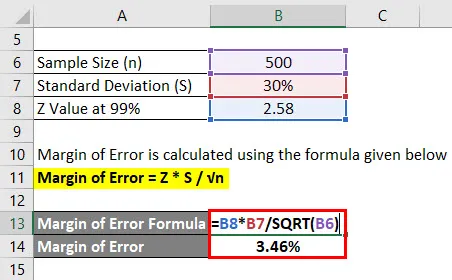
- Fejlmargin = 2, 58 * 30% / √ (500)
- Fejlmargin = 3, 46%
Dette betyder, at med 99% tillid er den gennemsnitlige karakter af studerende 2, 4 plus eller minus 3, 46%.
Margin of Error Formula - Eksempel # 2
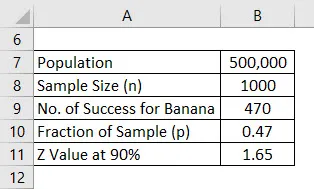
Lad os sige, at du lancerer et nyt sundhedsprodukt på markedet, men du er forvirret, hvilken smag folk vil kunne lide. Du er forvirret mellem banansmag og vaniljesmag og har besluttet at gennemføre en undersøgelse. Din befolkning for det er 500.000, som er dit målmarked, og ud af det besluttede du at spørge udtalelsen fra 1000 mennesker, og det vil prøve. Antag, at et konfidensinterval er 90%. Beregn fejlmargenen.
Løsning:
Når undersøgelsen er gennemført, fik du kendskab til, at 470 mennesker kunne lide banansmag, og 530 har bedt om vaniljesmag.
Fejlmargen beregnes ved hjælp af nedenstående formel
Fejlmargen = Z * √ ((p * (1 - p)) / n)
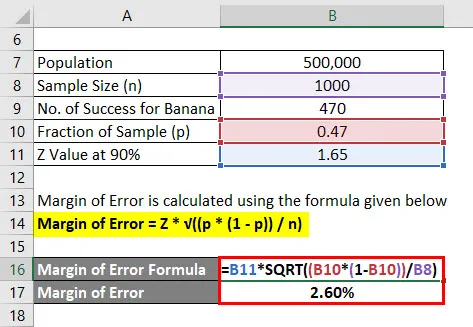
- Fejlmargin = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Fejlmargin = 2, 60%
Så vi kan sige, at med 90% tillid til, at 47% af alle mennesker kunne lide banansmag plus eller minus 2, 60%.
Forklaring
Som omtalt ovenfor hjælper fejlmargenen os med at forstå, om prøvestørrelsen på din undersøgelse er passende eller ej. I tilfælde af at marginfejlen er for stor, kan det være tilfældet, at vores stikprøvestørrelse er for lille, og vi er nødt til at øge det, så prøveresultaterne matcher tættere med populationsresultaterne.
Der er nogle scenarier, hvor fejlmargenen ikke vil være til stor nytte og ikke hjælper os med at spore fejlen:
- Hvis spørgsmålene i undersøgelsen ikke er designet og ikke hjælper med at få det krævede svar
- Hvis de personer, der besvarer undersøgelsen, har en vis bias med hensyn til det produkt, som undersøgelsen udføres for, er resultatet heller ikke særlig præcist
- Hvis den valgte prøve i sig selv er den rette repræsentant for befolkningen, vil også i dette tilfælde resultaterne være væk.
En stor antagelse her er også, at befolkningen normalt er fordelt. Så hvis prøvestørrelsen er for lille, og populationsfordelingen ikke er normal, kan z-score ikke beregnes, og vi kan ikke finde fejlmargenen.
Relevans og anvendelser af formel for margen af fejl
Hver gang vi bruger eksempeldata til at finde et relevant svar for populationssætet, er der en vis usikkerhed og chancer for, at resultatet afviger fra det faktiske resultat. Fejlmargenen fortæller os, at det, der er niveauet for afvigelse, der er, er prøveudgangen. Vi er nødt til at minimere fejlmargenen, så vores prøveresultater viser den faktiske historie om befolkningsdata. Så lavere fejlmargin, bedre vil resultaterne være. Fejlmargenen komplementerer og kompletterer de statistiske oplysninger, vi har. For eksempel, hvis en undersøgelse finder ud af, at 48% af befolkningen foretrækker at tilbringe tid hjemme i løbet af weekenden, kan vi ikke være så præcise, og der er nogle manglende elementer i denne information. Når vi introducerede en fejlmargin her, siger 5%, vil resultatet blive fortolket som 43-53% mennesker kunne lide ideen om at være hjemme i weekenden, hvilket giver fuld mening.
Margen for fejlformelberegner
Du kan bruge følgende margen for fejlberegner
| Z | |
| S | |
| √n | |
| Fejlmargen | |
| Fejlmargen | = |
|
|
Anbefalede artikler
Dette har været en guide til formlen Margin of Error. Her diskuterer vi, hvordan man beregner fejlmargen sammen med praktiske eksempler. Vi leverer også en Margin of Error-regnemaskine med downloadbar excel-skabelon. Du kan også se på de følgende artikler for at lære mere -
- Vejledning til formularer til ligefrem afskrivning
- Eksempler på formidling af fordoblingstid
- Hvordan beregnes amortisering?
- Formel til sætning af central grænse
- Altman Z Score | Definition | eksempler
- Afskrivningsformel | Eksempler med Excel-skabelon