Introduktion til Heap Sort i C
Sortering er en teknik, der handler om bestilling af elementer baseret på forskellige egenskaber. (Egenskaber som at arrangere data i stigende, faldende eller alfabetiske ordrer). Et vigtigt eksempel på sortering, som vi kan tænke på her, er bestilling af varer under online shopping. Vi kan forholde os til priser, popularitet, seneste og så videre. Så der er mange teknikker til denne positionering af elementer gennem sortering. I dette emne skal vi lære om Heap Sort i C.
Her skal vi lære en af de mest almindelige sorteringsteknikker, Heap Sort, gennem C-programmeringssprog.
Logikken for Heap Sort
Hvordan kan vi faktisk udføre heap sortering? Lad os tjekke nedenfor.
For det første er dyngen en af den træbaserede datastruktur. Træet, der er involveret her, er altid et komplet binærtræ. Og der er to slags bunke
- Min - Heap: Generelt arrangeret i stigende rækkefølge, det vil sige hvis det overordnede knudeelement har en værdi, der er mindre end værdien af underordnede elementer.
- Max - Heap: Generelt arrangeret i faldende rækkefølge, det vil sige hvis det overordnede knudeelement har en værdi mere end værdien af underordnede elementer.
Trin til Heap Sort
- Når en usorteret listedata er opnået, organiseres elementer i heapdatastrukturen enten baseret på oprettelse af en min-heap eller en max-heap.
- Det første element fra listen ovenfor tilføjes til vores array
- Igen efter dannelse af hoveddatatrukturteknikken, der er det samme som det første trin, følges igen og enten det højeste element eller det mindste element og samles i vores array.
- Gentagne trin hjælper os med at få matrixen med den sorterede liste.
Program for Heap Sort i C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Først beder vi brugeren om at indtaste antallet af elementer, der tages til sortering, og derefter får brugeren adgang til at indtaste forskellige elementer, der skal sorteres.
Trin fulgt
- Det næste, som vi fokuserer på, er at oprette et heap array, i dette tilfælde max-heap array.
- Hovedbetingelsen for at få en maksimal heap-array er at kontrollere, at ingen overordnede nodeværdi er mindre end dens underordnede værdi. Vi vil bytte, indtil vi opnår denne betingelse.
- Den største fordel i dette komplette binære træ er, at de venstre og højre underordnede knudepunkter i en overordnet knude er tilgængelige med henholdsvis værdier 2 (i) + 1 og 2 * (i) + 2-værdier. Hvor jeg er den overordnede knude.
- Så på den måde her placerer vi vores rodnode, der indeholder den maksimale værdi i det højre bladknudepunkt. Og derefter igen efter den samme procedure, således at det næste maksimale antal nu bliver rodnoden.
- Vi vil følge den samme procedure, indtil kun en knude er tilbage i bunken.
- Og så arrangerer vi vores heaparray til at danne et perfekt sorteret array i stigende rækkefølge.
- Endelig udskriver vi det sorterede array i output.
Produktion:
Outputet er vedhæftet nedenfor.
Lad mig vise dig den billedlige repræsentation af begivenhederne:
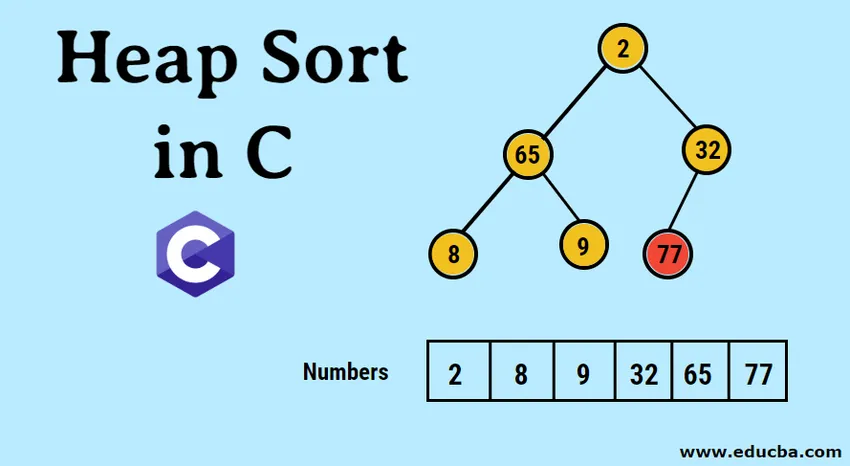
- De indtastede data repræsenteres først i form af en enkeltdimensionel matrix som følger.

- Den billedlige repræsentation af det dannede binære træ er som følger:
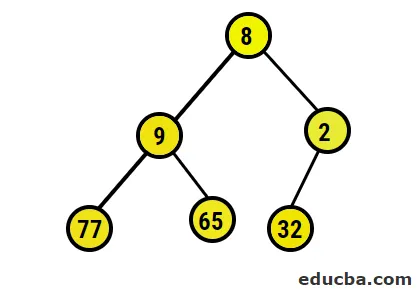
- Nu skal vi konvertere til den maksimale bunke ved at sikre os, at alle overordnede noder altid er større end underordnede noder. Som nævnt i output under heap-sorteret matrix, ville den billedlige repræsentation være:
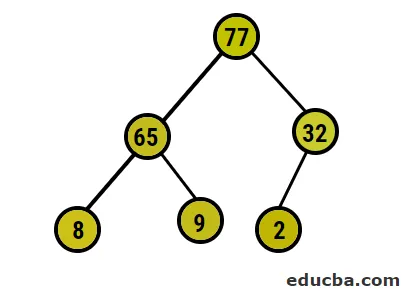
- Efter dette vil vi bytte rodnoden med den ekstreme bladknude og derefter slette den fra træet. Bladknuden ville være roden nu og igen samme proces e fulgt for igen at få det højeste element i roden
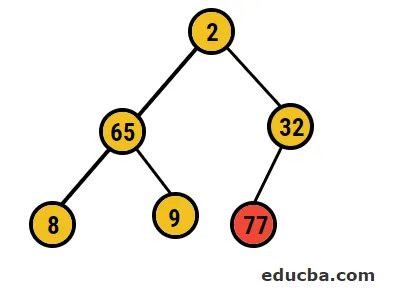
- Så i dette tilfælde slettes 77 cifre fra dette træ og placeres i vores sorterede array, og processen gentages.
Ovenstående har vi set det til dannelse af maksimal heap array. Den samme proces behandles også med dannelsen af min-heap array. Som diskuteret ovenfor er den eneste forskel i forholdet mellem forældre og børn knudeelementer.
Kan du som en øvelse prøve at forme dyngen i faldende rækkefølge?
Konklusion
Selvom der er mange sorteringsteknikker, betragtes heapsortering som en af de bedre sorteringsteknikker på grund af dets tid og rumkompleksitet. Tidskompleksiteten for alle bedst, gennemsnitlige og værste tilfælde er O (nlogn), hvor worst case-kompleksiteten er bedre end worst case-kompleksiteten i Quicksort, og rumkompleksiteten er O (1).
Anbefalede artikler
Dette er en guide til Heap Sort i C. Her diskuterer vi logikken og trinnene for Heap Sort med prøvekoden og output sammen med billedlige repræsentationer. Du kan også se på de følgende artikler for at lære mere -
- Heap sortering i Java
- Valgssortering i Java
- Palindrome in C-program
- Mønstre i C-programmering
- Heap sortering i C ++ (algoritme)
- Heap Sort i Python
- C Programmering af matrixmultiplikation