Introduktion til fletningssortering i Java
Program for Merge Sort i Java er en af de mest anvendte og effektive algoritmer. Flettsortering er baseret på opdelings- og erobringsteknik, som involverer at dele et givet problem i flere underproblemer og løse hvert underproblem uafhængigt. Når delproblemerne løses, kombinerer vi deres resultater for at få den endelige løsning på problemet. Flettsorteringsalgoritme kan implementeres ved hjælp af rekursion, da den involverer arbejde med underproblemer snarere end hovedproblemet.
Hvordan fungerer fletningen sortering?
Lad os overveje en usorteret matrix, der skal sorteres ved hjælp af flergesorteringsalgoritmen. Her er de trin, der er involveret i sortering af en matrix med værdier: 18, 8, 4, 13, 10, 12, 7 og 11:
- Det første trin involverer at finde et pivotelement, på grundlag af hvilket vores input-array bliver opdelt i undergrupper.
- Lad os overveje, at element 13 er valgt som drejepunkt, derfor vil det originale array opdeles i to undergrupper. Den første undergruppe vil indeholde 18, 8, 4, 13 og den anden undergruppe vil indeholde resterende elementer 10, 12, 7, 11.
- Subarrays opnået i trin 2 er yderligere opdelt som i trin 1, og dette fortsætter.
- Når hovedgruppen er opdelt i subarrays med enkeltelementer, begynder vi at flette disse subarrays igen, således at de fusionerede elementer er i sorteret rækkefølge.
- Sådan fungerer den egentlige kløft og erobring:
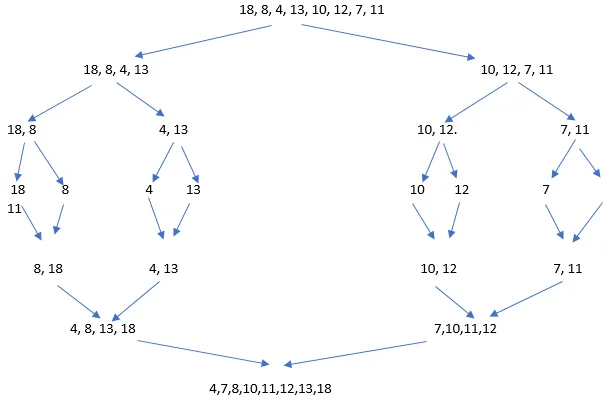
Program til fletningssortering i Java
Her er et kodeeksempel, der viser implementeringen af flettsortering i java:
Kode:
package com.edubca.sorting;
public class MergeSort (
private int() array;
private int() tempMergedArr;
private int length;
public static void main(String a())(
int() inputArr = (18, 8, 4, 13, 10, 12, 7, 11);
MergeSort mergeSort = new MergeSort();
mergeSort.sort(inputArr);
for(int i:inputArr)(
System.out.print(i + " ");
)
)
public void sort(int inputArr()) (
this.array = inputArr;
this.length = inputArr.length;
this.tempMergedArr = new int(length);
performMergeSort(0, length - 1);
)
private void performMergeSort(int lowerIndex, int higherIndex) (
if (lowerIndex < higherIndex) (
int middle = lowerIndex + (higherIndex - lowerIndex) / 2;
// Sort the left side of the array call performMergeSort recursively
performMergeSort(lowerIndex, middle);
// Sort the right side of the array call performMergeSort recursively
performMergeSort(middle + 1, higherIndex);
// Merge subparts using a temporary array
mergeData(lowerIndex, middle, higherIndex);
)
)
private void mergeData (int lowerIndex, int middle, int higherIndex) (
for (int i = lowerIndex; i <= higherIndex; i++) (
tempMergedArr(i) = array(i);
)
int i = lowerIndex;
int j = middle + 1;
int k = lowerIndex;
while (i <= middle && j <= higherIndex) (
if (tempMergedArr(i) <= tempMergedArr(j)) (
array(k) = tempMergedArr(i);
i++;
) else (
array(k) = tempMergedArr(j);
j++;
)
k++;
)
while (i <= middle) (
array(k) = tempMergedArr(i);
k++;
i++;
)
)
)
Ovenstående kode producerer en sorteret matrix som output.
Produktion:

Hvornår skal vi bruge fletningen Sort?
Flettesortering kan bruges i følgende scenarier:
- Når datastrukturen, der skal sorteres, ikke understøtter tilfældig adgang, kan flettsorteringen være nyttig og effektiv.
- Når der kræves et højt niveau af parallelisme, kan fletningssortering bruges, da forskellige underproblemer kan løses uafhængigt ved hjælp af flere processer, der kører parallelt.
- Flettesortering er hurtigere, når du arbejder med sammenkædede lister, fordi pegere let kan ændres, mens listerne slås sammen.
- Merge Sort kan betragtes som en stabil sortering, hvilket betyder, at det samme element i en matrix opretholder deres originale positioner i forhold til hinanden. I tilfælde, hvor høj stabilitet er påkrævet, kan man gå til sortering.
Kompleksitetsanalyse af sammensnitssortering
Nedenfor punkter analyserer kompleksiteten af fletningssortering:
- Flettesortering er en rekursiv algoritme, og dens tidskompleksitet er O (n * log n) i alle de tre tilfælde (værst, bedst og gennemsnit), da fletningssorter deler arrayet i to lige store halvdele og tager lineær tid at flette dem.
- Rumkompleksitet ved fletningssortering er O (n), da det fungerer på den rekursive tilgang. Flettsortering kan derfor betragtes som hurtig, plads- og tidseffektiv algoritme.
Sammenligning af fusionssortering med andre algoritmer
Nedenfor punkter sammenligner fletningssortering med andre algoritmer:
- Heap Sort har samme tidskompleksitet som fletningssortering, men det kræver kun O (1) hjælpeplads i stedet for flettesorterings O (n). Derfor er heapsortering mere pladseffektiv end sammenfletningssortering.
- Hurtigsorteringsimplementeringer overgår generelt mere sammenfletningssortering til sortering af RAM-baserede arrays.
- Flet sorterer bedre end hurtig sortering og heap sorteringsalgoritmer, når du arbejder med den tilknyttede liste, da pegere let kan ændres.
Konklusion-program for fletningssortering i Java
Fra artiklen konkluderes det, at fletningssorten er et vigtigt begreb at forstå, når det kommer til algoritmer.
Anbefalede artikler
Dette er en guide til Program til fletningssortering i Java. Her diskuterer vi, hvordan skal dets arbejde, dets anvendelse, programmet til sammenfletningssortering osv. Du kan også gennemgå vores andre relaterede artikler for at lære mere-
- Flet sortering i Java
- Flet sorteringsalgoritmer i Java
- Heap Sort in C
- Heap sortering i Java
- Java-implementeringsværktøjer
- Heap Sort i Python
- Hurtig sorteringsalgoritmer i Java
- Top 6 sorteringsalgoritme i JavaScript
- Top 6 sorteringsalgoritmer i Python