
Definition af middeleksempel
Gennemsnit i den statistiske parlance kan omtales som det matematiske aritmetiske eller geometriske gennemsnit, der kan beregnes for et sæt på 2 eller flere rettidige afkast.
Der som nævnt i definitionen er der imidlertid mere end en enkelt måde til beregning af gennemsnittet eller middelværdien for et bestemt givet datasæt eller givet et sæt tal, der skal omfatte metoderne for det geometriske middelværdi og det aritmetiske middelværdi .
Ligningen eller formlen for et gennemsnit eller gennemsnit af afkast baseret på det aritmetiske gennemsnit kan beregnes ved at opsummere alle de tilgængelige periodiske afkast eller alle de givne observationer og dele det resultat med antallet af observationer eller antallet af perioder.
Eksempler på middelværdi
Nedenfor er eksemplerne på middelværdien:
Middeleksempel 1
XYZ-aktien har haft ret gode resultater i et par år, men investorerne er lidt skeptiske over for, om bestanden ville fungere det samme i fremtiden, da de i de seneste uger har forblevet ustabile, da et af selskabets nøglepersoner har trukket sig tilbage og markedet er begyndt at tvivle om virksomhedens fremtid.
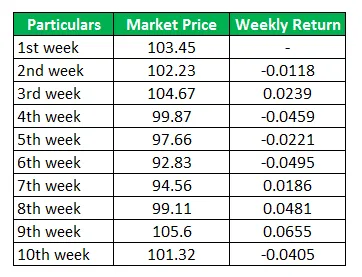
Axel ønsker at investere i XYZ-aktier og har henvendt sig til finansiel rådgiver for at rådgive om XYZ-aktier. Før rådgiveren beregner gennemsnittet af de ugentlige returneringer.
Løsning:
Vi får ugentlig afkast af XYZ-bestanden, og nu skal vi beregne gennemsnittet af disse ugentlige data, der er i 9 uger.
Formlen til beregning af gennemsnittet eller gennemsnitligt afkast er summen af alle data og divideret det samme med et antal observationer. og antallet af observationer er 9
Gennemsnit = I alt / antal observationer
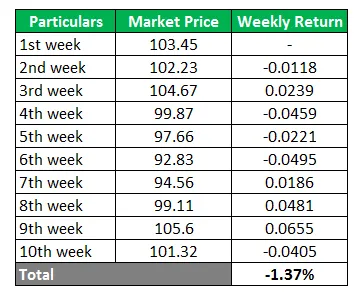
Gennemsnit = -1, 37% / 9
Gennemsnit = -0, 15%
Derfor vil det gennemsnitlige ugentlige afkast være -1, 37% ved at dividere det samme med 9 giver -0, 15% gennemsnitligt afkast for XYZ-aktien.
Middeleksempel -2
Suhas er administrerende direktør for Vatsal-virksomhederne, og han ser, at hans salg er varierende for hver måned, og han vil vide gennemsnitligt kvartalsalg og ønsker at identificere det kvartal, hvor salget er mest.
Nedenfor er de månedlige salgsdata, der er uddraget fra regnskabssoftware. Det kræves, at du beregner det kvartalsvise aritmetiske gennemsnit.
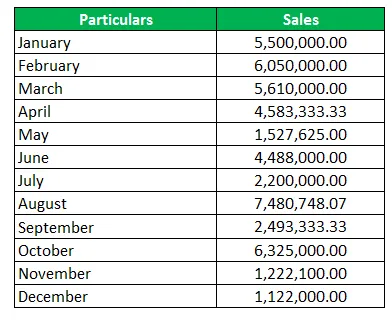
Løsning:
Vi får et månedligt salg, og derfor tager vi summen af 3 måneder, der starter fra januar, og derefter for hver total, deler vi det med 3, hvilket giver os det gennemsnitlige salgstall for kvartalet.
Gennemsnit = I alt / antal observationer
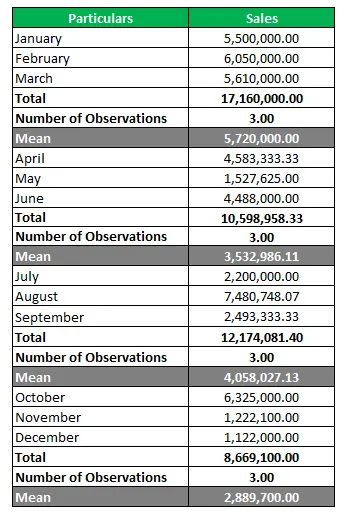
Det højeste gennemsnit er for 1. kvartal, og derfor er dette kvartal det bedst mulige for virksomheden.
Middeleksempel -3
Jack Hemsley er for nylig uddannet, og hans interesseområde ligger på aktiemarkedet. Han har observeret Alpha-aktier i lang tid og ønsker at beregne det daglige gennemsnitlige afkast, da han føler, at han nu kan handle ind i det samme og kan tjene penge på det. Hans ven Jill råder ham først til at vide, hvilket afkast han kan forvente, når han begynder at handle, og derfor foreslår han ham at beregne gennemsnittet, som denne aktie har givet. Jack beslutter at bruge et geometrisk gennemsnit på over aritmetisk gennemsnit. Det kræves, at du beregner geometrisk gennemsnit baseret på nedenstående data for de sidste 5 dage.
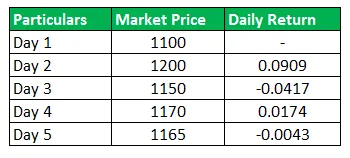
Løsning:
For at beregne geometrisk retur, er vi nødt til at tage produktet af returen og derefter tage den fjerde rod af resultatet og trække det samme fra 1 giver os det geometriske afkast.
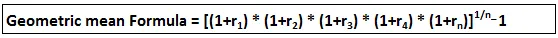
- Geometrisk middelværdi = ((1 + 0, 0909) * (1-0.0417) * (1 + 0.0174) * (1-0.0043)) 1/4 - 1
- Geometrisk middelværdi = 1, 45%
Middeleksempel -4
Nedenfor er eksemplet på 5 børn, der bliver 10 år gamle, og deres højdedata er givet. Det kræves, at du beregner både det aritmetiske middelværdi og det geometriske middelværdi og sammenligner begge og kommenterer det samme.
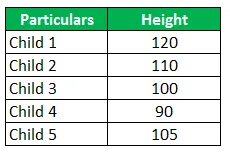
Løsning:
For at beregne geometrisk retur, er vi nødt til at tage produktet fra observationer og derefter tage den 5. rot af resultatet og trække det samme fra 1 giver os det geometriske afkast.
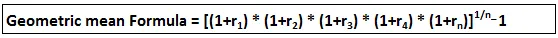
- Geometrisk middelværdi = ((1 + 120) * (1 + 110) * (1 + 100) * (1 + 90) * (1 + 105)) 1/5 - 1
- Geometrisk middelværdi = 104, 52
Formlen til beregning af gennemsnittet eller middelafkastet er summen af alle data og divideret det samme med antallet af observationer, og antallet af observationer er 5.
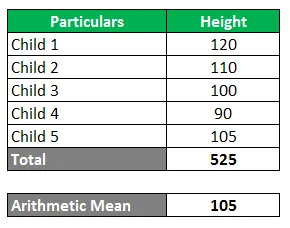
Aritmetisk gennemsnit = I alt / antal observationer
- Aritmetisk gennemsnit = 525/5
- Aritmetisk gennemsnit = 105
Geometrisk middelværdi er mindre end det aritmetiske middel og er generelt tilfældet, og det kan ikke være mere end det aritmetiske middelværdi.
Konklusion - middeleksempel
Gennemsnit eller middelværdi bruges og beregnes næsten dagligt og af mange forskellige grunde, især inden for kapitalmarkedet, videnskab, statistik osv. Brug af det passende gennemsnit er nøglen, og denne sag er baseret på en forståelse af dataene. Det geometriske gennemsnit overvejer sammensætning, mens det aritmetiske gennemsnit overvejer enkel summering. Derfor er vækst forventes at være kendt geometrisk bedst, og hvor værdier ikke er meget flygtige og ikke meget spredt aritmetisk gennemsnit kan anvendes.
Anbefalede artikler
Dette har været en guide til middeleksemplet. Her har vi diskuteret definitionen sammen med forskellige eksempler på middelværdi med geometrisk middelværdi og aritmetisk gennemsnit. Du kan også se på de følgende artikler for at lære mere -
- Eksempel på faste omkostninger
- Variabel omkostningseksempel
- Kvantitativt eksempel
- Eksempler på monopolistisk konkurrence